Γιατί ... ... ο χρόνος τρέχει πιο αργά στις υψηλές ταχύτητες;

 

Γιατί ... ... ο χρόνος τρέχει πιο αργά στις υψηλές ταχύτητες;

Μια προσπάθεια εξήγησης της χρονικής διαστολής του Αϊνστάιν με απλό τρόπο

ΣΦΑΙΡΙΚΗ ΕΙΚΟΝΑ

1. Τα θεμέλια της ειδικής θεωρίας της σχετικότητας
2. Το φαινόμενο Doppler
3. Ένα παράδειγμα διαστολής χρόνου
4. Διαστολή χρόνου, εξεταζόμενη με περισσότερες λεπτομέρειες

Πιθανότατα έχετε ήδη ακούσει ότι η ταχύτητα κενού του φωτός c = 299 792 458 m/s παίζει ιδιαίτερο ρόλο στη φυσική. Εκτός από το ορατό φως, τα ραδιοκύματα, οι υπέρυθρες, οι υπεριώδεις, οι ακτίνες Χ και οι ακτίνες γάμμα ταξιδεύουν επίσης με την ταχύτητα του φωτός στο κενό. Είναι επίσης γνωστό ότι κανένα υλικό αντικείμενο (εκτός από το διαστημόπλοιο Enterprise?) δεν μπορεί να φτάσει ή και να ξεπεράσει την ταχύτητα του φωτός. Όταν πλησιάζει η ταχύτητα του φωτός, συμβαίνουν ασυνήθιστα φαινόμενα, τα οποία ο διάσημος φυσικός Άλμπερτ Αϊνστάιν είχε προβλέψει ήδη από το 1905 στην ειδική θεωρία της σχετικότητας .

Ένα συμπέρασμα από τη θεωρία του Αϊνστάιν είναι ιδιαίτερα εντυπωσιακό:

Όταν κινείστε σχεδόν με την ταχύτητα του φωτός, ο χρόνος τρέχει πολύ πιο αργά.

Στη συνέχεια θα ήθελα να προσπαθήσω να εξηγήσω αυτό το γεγονός όσο το δυνατόν πιο απλά (αλλά και πάλι σωστά) χρησιμοποιώντας ένα παράδειγμα.

1. Βασικές αρχές της ειδικής θεωρίας της σχετικότητας

Η Φυσική χρησιμοποιεί μια χρονική κλίμακα και ένα χωρικό σύστημα συντεταγμένων (π.χ. ένα καρτεσιανό σύστημα συντεταγμένων με τρεις αμοιβαία κάθετους άξονες) για να περιγράψει μια διαδικασία. Ο χρόνος μηδέν μπορεί να οριστεί αυθαίρετα (π.χ. στη γέννηση του Χριστού). Όσον αφορά το σύστημα χωρικών συντεταγμένων, οι κατευθύνσεις αρχής και άξονα μπορούν να επιλεγούν αυθαίρετα. Είναι επίσης δυνατό να χρησιμοποιηθεί ένα «κινούμενο» σύστημα συντεταγμένων , δηλαδή να περιγράψει την κίνηση των δέντρων (!) από την οπτική γωνία ενός αυτοκινήτου.

Όταν μιλάμε για συστήματα συντεταγμένων ή συστήματα αναφοράς παρακάτω, εννοούμε πάντα τα λεγόμενα αδρανειακά συστήματα , τα οποία είναι συστήματα αναφοράς στα οποία σώματα χωρίς δύναμη παραμένουν σε ηρεμία σύμφωνα με το νόμο της αδράνειας ή κινούνται με σταθερή ταχύτητα και κατεύθυνση. Χαρακτηριστικό παράδειγμα αδρανειακού συστήματος είναι το σύστημα αναφοράς ενός διαστημόπλοιου που πετά χωρίς πρόωση, στο οποίο οι αστροναύτες βρίσκονται σε κατάσταση έλλειψης βαρύτητας. (Σε ένα μη αδρανειακό πλαίσιο, από την άλλη πλευρά, θα υπάρχουν αδρανειακές δυνάμεις, όπως το ξαφνικό φρενάρισμα ενός αυτοκινήτου, ή φυγόκεντρες δυνάμεις, όπως στο περιστρεφόμενο τρενάκι.)

Η ειδική θεωρία της σχετικότητας ασχολείται ουσιαστικά με το ακόλουθο ερώτημα:

Σε ποιο βαθμό μπορούν τα φυσικά μεγέθη να έχουν διαφορετικές τιμές σε συστήματα συντεταγμένων που κινούνται αμοιβαία;

Η εξάρτηση από το σύστημα αναφοράς είναι προφανής για την ταχύτητα: Εάν το σύστημα συντεταγμένων που χρησιμοποιείται είναι συνδεδεμένο με ένα σταθμευμένο αυτοκίνητο, για παράδειγμα, τα δέντρα στην άκρη του δρόμου έχουν ταχύτητα 0 km/h . Αν κοιτάξετε τα ίδια δέντρα στο σύστημα αναφοράς ενός πεζού ή ενός κινούμενου αυτοκινήτου, αυτά τα δέντρα (!) κινούνται με 5 km/h ή 100 km/h, για παράδειγμα. (Πιθανή φράση από τον Αϊνστάιν: "Πότε θα σταματήσει η Ουλμ σε αυτό το τρένο;")

Από την άλλη πλευρά, φαίνεται αδιανόητο η «κοινή λογική» ότι το μήκος, ο χρόνος ή η μάζα θα μπορούσαν να εξαρτώνται από το σύστημα συντεταγμένων που χρησιμοποιείται. Ο Άλμπερτ Αϊνστάιν ήταν ο πρώτος που είχε την επαναστατική ιδέα ότι αυτές οι ποσότητες θα μπορούσαν επίσης να αλλάξουν με το σύστημα αναφοράς. Στις σκέψεις του, ο Αϊνστάιν ξεκίνησε από δύο αρχές, την αρχή της σχετικότητας και την αρχή της σταθερότητας της ταχύτητας του φωτός :

αρχή της σχετικότητας

Οι νόμοι της φύσης έχουν την ίδια μορφή σε δύο διαφορετικά συστήματα αναφοράς που κινούνται με τον ίδιο ρυθμό μεταξύ τους (δηλαδή με σταθερή ταχύτητα και την ίδια κατεύθυνση κίνησης). Αυτά τα συστήματα αναφοράς είναι επομένως ίσα.

Αυτή η αρχή της σχετικότητας βρίσκεται ήδη στην κλασική ( Νευτώνεια ) Με βάση τη μηχανική. Ένα παράδειγμα είναι η προσπάθεια να προσδιοριστεί μέσω φυσικών μετρήσεων σε διαμέρισμα τρένου (χωρίς παράθυρα, με πλήρη ηχομόνωση, τέλεια ανάρτηση, απολύτως επίπεδη τροχιά κ.λπ.) εάν το τρένο κινείται ή ποια είναι η ταχύτητά του. Σύμφωνα με τη Νευτώνεια μηχανική αυτό είναι αδύνατο. Από την άλλη πλευρά, η επιτάχυνση ή η στροφή του τρένου μπορεί εύκολα να αναγνωριστεί, για παράδειγμα από μια μπάλα στο πάτωμα του σιδηροδρομικού βαγονιού που αρχίζει να κινείται. Αν κάποιος χρησιμοποιεί δύο διαφορετικά συστήματα αναφοράς στη Νευτώνεια μηχανική, τα οποία κινούνται ομοιόμορφα μεταξύ τους, τότε λαμβάνονται διαφορετικές τιμές για μετρήσεις ταχύτητας, αλλά οι ίδιες τιμές λαμβάνονται για μετρήσεις επιτάχυνσης.

Είναι σημαντικό για την κατανόηση της αρχής της σχετικότητας να υποτεθεί η απουσία εξωτερικών δυνάμεων (π.χ. βαρυτικών δυνάμεων). Γενικά, διαφορετικά συστήματα αναφοράς στη γη που κινούνται μεταξύ τους δεν μπορούν να θεωρηθούν ίσα. Αν, από την άλλη πλευρά, κάποιος θεωρήσει δύο πύραυλους που πετούν ο ένας δίπλα στον άλλο σε μεγάλη απόσταση από το πλησιέστερο ουράνιο σώμα, τα συστήματα συντεταγμένων που σχετίζονται με αυτούς τους πύραυλους είναι ίσα. Για παράδειγμα, καθένα από τα δύο πληρώματα πυραύλων μπορεί να ισχυριστεί ότι το δικό του διαστημόπλοιο κινείται με 100 km/s ενώ ο άλλος πύραυλος είναι ακίνητος. Για παράδειγμα, ένας άλλος παρατηρητής θα μπορούσε να πει με την ίδια αιτιολόγηση ότι ο πρώτος πύραυλος ταξίδευε με ταχύτητα 20 km/sπρος μία κατεύθυνση και το δεύτερο προς την αντίθετη κατεύθυνση με 80 km/s .

Συμπέρασμα: Η κίνηση είναι ένας σχετικός όρος (δηλαδή εξαρτάται από το σύστημα αναφοράς που χρησιμοποιείται). Δεν υπάρχει απόλυτος χώρος.

Η δεύτερη αρχή στην οποία βασίζεται η ειδική θεωρία της σχετικότητας προβλέφθηκε από τον James Clerk Maxwell στη Θεωρία της Ηλεκτροδυναμικής (1861 έως 1864) και επιβεβαιώθηκε πειραματικά για πρώτη φορά το 1881 από τον Albert Abraham Michelson :

Αρχή της σταθερότητας της ταχύτητας του φωτός

Η ταχύτητα κενού του φωτός  c έχει την ίδια τιμή σε κάθε πλαίσιο αναφοράς.

Αυτή η αρχή έχει εκπληκτικές συνέπειες. Εάν ένας παρατηρητής πλησιάσει μια πηγή ήχου με τη μισή ταχύτητα του ήχου και μετρήσει την ταχύτητα του εισερχόμενου ήχου στο πλαίσιο αναφοράς του, θα πάρει μιάμιση φορά την κανονική τιμή. Από την άλλη πλευρά, για έναν παρατηρητή που πλησιάζει μια φωτεινή πηγή με τη μισή ταχύτητα του φωτός, η ταχύτητα του εισερχόμενου φωτός έχει μόνο την κανονική τιμή στο πλαίσιο αναφοράς του.

2. Το φαινόμενο Doppler

Όλοι έχουν παρατηρήσει καθώς περνάει ένα ασθενοφόρο, ότι η έκρηξη της σειρήνας πέφτει ξαφνικά στον αγωνιστικό χώρο καθώς το ασθενοφόρο περνάει. Αυτό το φαινόμενο ονομάζεται φαινόμενο Doppler (από το όνομα του Αυστριακού φυσικού Christian Doppler ) και είναι χαρακτηριστικό για τη διάδοση κυμάτων, για παράδειγμα ηχητικών ή φωτεινών κυμάτων. Πώς προκύπτει αυτό το αποτέλεσμα;

Η πηγή ήχου εκπέμπει μέτωπα κυμάτων σε ένα ορισμένο χρονικό διάστημα (π.χ. 0,0020 s) , τα οποία διαδίδονται προς όλες τις κατευθύνσεις με ταχύτητα περίπου 330 m/s . Εάν η πηγή ήχου κινηθεί προς τον παρατηρητή, τα μέτωπα των κυμάτων που εκπέμπονται αργότερα έχουν μικρότερη απόσταση για να καλύψουν τον παρατηρητή και επομένως χρειάζονται λιγότερο χρόνο για να φτάσουν σε αυτόν. Ως αποτέλεσμα, τα μέτωπα των κυμάτων φτάνουν στον παρατηρητή σε μικρότερο χρονικό διάστημα (π.χ. 0,0018 s) . Αντιλαμβανόμαστε αυτή την ταχύτερη διαδοχή των μετώπων κυμάτων ως αύξηση του τόνου.

Εάν η πηγή ήχου απομακρυνθεί από τον παρατηρητή, τα μέτωπα κυμάτων που εκπέμπονται αργότερα χρειάζονται περισσότερο χρόνο για να φτάσουν στον παρατηρητή λόγω της μεγαλύτερης διαδρομής. Με αυτόν τον τρόπο, η χρονική απόσταση των μετώπων κυμάτων αυξάνεται (π.χ. σε 0,0022 s). Σε αυτή την περίπτωση, αντιλαμβανόμαστε χαμηλότερο τόνο. Στο αριθμητικό παράδειγμα που δόθηκε τελευταίο, ο συντελεστής επιμήκυνσης για το χρονικό διάστημα μεταξύ των μετώπων κυμάτων είναι k = 0,0022 s / 0,0020 s = 1,1.

Αντίστοιχο αποτέλεσμα εμφανίζεται και με τα φωτεινά κύματα. Εάν η πηγή φωτός πλησιάζει τον παρατηρητή, τα μέτωπα των κυμάτων φτάνουν στον παρατηρητή σε μικρότερο χρονικό διάστημα (μετατόπιση ιώδους). Στην αντίθετη περίπτωση, παρατηρείται μετατόπιση κόκκινου χρώματος. (Ένα διάσημο παράδειγμα είναι η ερυθρή μετατόπιση στο φως των γαλαξιών που απομακρύνονται από τον Γαλαξία μας. Αυτή η μετατόπιση στο κόκκινο θεωρείται απόδειξη για τη θεωρία της Μεγάλης Έκρηξης.)

Εάν η ταχύτητα της πηγής φωτός σε σχέση με τον παρατηρητή γίνει παρόμοια με την ταχύτητα του φωτός, το φαινόμενο Doppler μπορεί να έχει ακραία επίδραση. Αυτό εξηγείται με περισσότερες λεπτομέρειες χρησιμοποιώντας το ακόλουθο παράδειγμα:

παράδειγμα 1

Το έτος 2500, ένας μη επανδρωμένος διαστημικός ανιχνευτής εκτοξεύεται με ταχύτητα v = 0,8 c (δηλαδή με 0,8 φορές την ταχύτητα του φωτός) προς το μακρινό νεφέλωμα της Ανδρομέδας. Κάθε χρόνο, ο επίγειος σταθμός στη Γη στέλνει ένα ραδιοφωνικό σήμα (με την ταχύτητα του φωτός) στο διαστημόπλοιο. Κάθε φορά που φθάνει ένα τέτοιο σήμα, ο ενσωματωμένος υπολογιστής καταγράφει την ώρα (προφανώς μετρούμενη από το ρολόι του διαστημικού σκάφους) και στέλνει ένα σήμα απάντησης πίσω στη Γη ως επιβεβαίωση.

Όπως φαίνεται από το διαστημόπλοιο, η Γη συμπεριφέρεται σαν μια πηγή φωτεινού σήματος που απομακρύνεται από το διαστημόπλοιο. Γνωρίζουμε ήδη ότι οι χρόνοι άφιξης σήματος που καταγράφονται από τον ενσωματωμένο υπολογιστή πρέπει να έχουν διαφορά μεγαλύτερη από ένα χρόνο. Τώρα όμως πρέπει να υπολογιστεί ακριβώς πόσο μεγάλο είναι αυτό το χρονικό διάστημα. Θέλουμε λοιπόν να γνωρίζουμε τον παράγοντα επιμήκυνσης k για το χρονικό διάστημα μεταξύ των σημάτων.

Τα σήματα που στέλνει η γη κάθε χρόνο (χρόνος της γης!) φτάνουν στον διαστημικό ανιχνευτή σε διάστημα k ετών (χρόνος διαστημικού ανιχνευτή!). Η ποσότητα k εξαρτάται από την ταχύτητα v . Μέχρι στιγμής γνωρίζουμε μόνο ότι το k πρέπει να είναι μεγαλύτερο από 1.

Τώρα εξετάζουμε τη διάδοση των σημάτων απόκρισης από την προοπτική της γης. Με αυτόν τον τρόπο, ο διαστημικός ανιχνευτής είναι μια πηγή φωτεινού σήματος που εκπέμπει τα σήματα του σε διαστήματα k ετών και απομακρύνεται από τη Γη με ταχύτητα v = 0,8 c . Σύμφωνα με την αρχή της σχετικότητας , τα συστήματα αναφοράς της γης και του διαστημικού ανιχνευτή είναι ίσα. Πρέπει επομένως να ισχύει ο ίδιος νόμος για τα σήματα απόκρισης από τον διαστημικό ανιχνευτή με τα αρχικά σήματα που προέρχονται από τη γη: πρέπει να φθάνουν (σύμφωνα με τον χρόνο της γης!) σε k φορές μεγαλύτερο χρονικό διάστημα από αυτό που στάλθηκαν από τον διαστημικό ανιχνευτή ( σύμφωνα με το χρόνο του διαστημικού ανιχνευτή!), δηλαδή σε διάστημα k · k ετών. Από το διάγραμμα χρονικής μετατόπισης (διάγραμμα ts)Ωστόσο, αυτό το χρονικό διάστημα μπορεί να διαβαστεί απευθείας: είναι ακριβώς 9 χρόνια. Με αυτό μπορούμε να καθορίσουμε το μέγεθος του k. Από k · k = 9 προκύπτει αμέσως ότι k = 3.

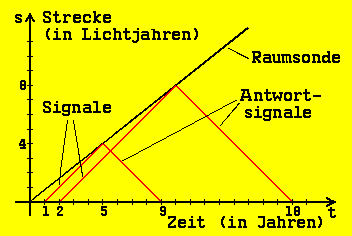
Μια αντίστοιχη θεώρηση για ένα αεροσκάφος με 0,8 φορές την ταχύτητα του ήχου, το οποίο λαμβάνει ηχητικά σήματα και τα στέλνει αμέσως πίσω, θα ήταν λάθος: η ταχύτητα του ήχου θα είχε την κανονική τιμή στο σύστημα επίγειων σταθμών, ενώ στο σύστημα του αεροσκάφους λάβετε μόνο 0,2 φορές αυτή την ταχύτητα που θα καταγραφόταν. (Υπάρχει μια αρχή της σταθερότητας της ταχύτητας του φωτός , αλλά καμία αρχή της σταθερότητας της ταχύτητας του ήχου.) Ένας διαφορετικός συντελεστής επιμήκυνσης k θα ίσχυε επομένως στα σήματα απόκρισης από ότι στα αρχικά σήματα.

Αποτέλεσμα του παραδείγματος 1

Εάν μια πηγή σήματος, η οποία εκπέμπει τακτικά φωτεινά σήματα σε ένα ορισμένο χρονικό διάστημα, απομακρυνθεί από τον παρατηρητή με ταχύτητα v = 0,8 c , ο παρατηρητής καταγράφει τα σήματα σε χρονικό διάστημα που είναι τρεις φορές μεγαλύτερο.   Αντίστοιχα, μπορεί κανείς να θεωρήσει ότι στην περίπτωση μιας πηγής σήματος που έρχεται πιο κοντά στον παρατηρητή με v = 0,8 c , το χρονικό διάστημα μεταξύ των επιμέρους σημάτων μειώνεται στο ένα τρίτο της αρχικής τιμής.

Ένας διαφορετικός συντελεστής επιμήκυνσης k φυσικά θα είχε ως αποτέλεσμα διαφορετική τιμή ταχύτητας v . Με λίγα μαθηματικά, μπορεί να προκύψει ο ακόλουθος τύπος:

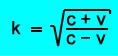
k ... συντελεστής επέκτασης για το χρονικό διάστημα μεταξύ των σημάτων
v ... ταχύτητα της πηγής σήματος σε σχέση με τον παρατηρητή
γ ... ταχύτητα φωτός υπό κενό

Αυτός ο τύπος δίνει επίσης το παραπάνω αποτέλεσμα για v = 0,8 c :

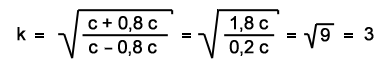
3. Ένα παράδειγμα διαστολής χρόνου

παράδειγμα 2

Την 1η Ιανουαρίου 3000, ορισμένοι αστροναύτες που ενδιαφέρονται για τη λογοτεχνία φεύγουν από τη Γη για έναν πλανήτη 4 έτη φωτός μακριά για να απολαύσουν μια ανάγνωση ποίησης του Vogon (δείτε τον Douglas Adams για περισσότερα σχετικά με την ποίηση του Vogon ). Η ταχύτητα πλεύσης είναι v = 0,8 c, έτσι ώστε η πτήση προς τα έξω και την επιστροφή να διαρκεί 5 χρόνια (χρόνος της γης, όχι χρόνος διαστημόπλοιου!). Ο επίγειος σταθμός στη γη στέλνει χαιρετισμό Πρωτοχρονιάς την 1η Ιανουαρίου των επόμενων ετών.

Χρησιμοποιώντας το φαινόμενο Doppler, στο οποίο υπόκεινται επίσης αυτά τα σήματα, μπορούμε να μάθουμε πόσος χρόνος μεσολαβεί κατά τη διάρκεια της πτήσης για τους αστροναύτες. Χρησιμοποιούμε ένα διάγραμμα ts που δείχνει την κίνηση του διαστημικού σκάφους και τα ραδιοσήματα στο πλαίσιο αναφοράς της γης.

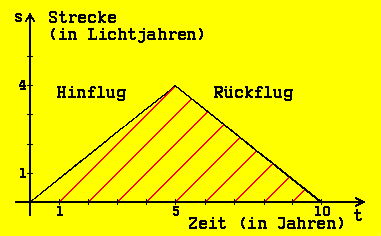
Όπως μπορείτε να δείτε, το πλήρωμα έλαβε τα συγχαρητήρια της 1ης Ιανουαρίου 3001 μόνο στο σημείο καμπής.

Πρώτον, η πτήση προς τα έξω θα πρέπει να εξεταστεί από τη σκοπιά του πληρώματος του διαστημικού σκάφους. Η γη ως πηγή σήματος απομακρύνεται με v = 0,8 c, έτσι ώστε τα συγχαρητήρια σήματα της να μην φτάνουν κάθε χρόνο, αλλά κάθε τρία χρόνια λόγω του φαινομένου Doppler (όπως φαίνεται παραπάνω ). Αυτό καθιστά σαφές ότι το ρολόι του διαστημόπλοιου δείχνει την 1η Ιανουαρίου 3003 στο σημείο αντιστροφής . Από τη σκοπιά της γης όμως, η ανατροπή γίνεται την 1η Ιανουαρίου 3005 (βλ. διάγραμμα )! Αυτό δείχνει για πρώτη φορά ότι η διάρκεια μιας διαδικασίας μπορεί να ποικίλλει σε διαφορετικά συστήματα αναφοράς.

Η πτήση επιστροφής θα πρέπει επίσης να λαμβάνεται υπόψη στο σύστημα αναφοράς του διαστημόπλοιου. Η γη ως πηγή σήματος πλησιάζει τώρα το διαστημόπλοιο με v = 0,8 c , έτσι ώστε τα συγχαρητήρια σήματα τους να μην φτάνουν σε διάστημα ενός έτους, αλλά αυτή τη φορά σε διάστημα ενός τρίτου του έτους. Τώρα το μόνο που έχετε να κάνετε είναι να διαβάσετε τον αριθμό των διαστημάτων του τρίτου έτους στο διάγραμμα : υπάρχουν εννέα τέτοιες περίοδοι. Σύμφωνα με αυτό, η πτήση επιστροφής σε χρόνο διαστημόπλοιου (όπως αναμενόταν) διαρκεί ακριβώς όσο και η πτήση προς τα έξω, δηλαδή τρία χρόνια.

Αποτέλεσμα του παραδείγματος 2

Εάν το διαστημόπλοιο πετάξει από και προς τον πλανήτη 4 έτη φωτός μακριά με ταχύτητα v = 0,8c , περνούν μόνο 6 χρόνια για το πλήρωμα , ενώ στη Γη ο χρόνος αυξάνεται κατά 10 χρόνια .

Ο τεχνικός όρος για αυτή τη "διαστολή χρόνου" είναι διαστολή χρόνου .

Συμπέρασμα: Ο χρόνος είναι σχετικός όρος (δηλαδή εξαρτάται από το σύστημα αναφοράς που χρησιμοποιείται). Δεν υπάρχει απόλυτος χρόνος.

4. Χρονική διαστολή, εξεταζόμενη με περισσότερες λεπτομέρειες

Έχουμε φτάσει στο τέλος των προβληματισμών μας, σχεδόν τουλάχιστον. Ωστόσο, μια σημαντική λεπτομέρεια μένει να διευκρινιστεί. Στο τελευταίο μας παράδειγμα, το κινούμενο ρολόι στο διαστημόπλοιο είναι πιο αργό από τα ρολόγια στη Γη. Από την άλλη πλευρά , γνωρίζουμε ότι η κίνηση είναι μια σχετική έννοια. Μπορούμε επομένως να πάρουμε τη θέση ότι το διαστημόπλοιο είναι ακίνητο όλη την ώρα και η γη κινείται μπρος-πίσω. Δεν είναι αντίφαση;

Στην πραγματικότητα, τα συστήματα αναφοράς της γης και του διαστημόπλοιου δεν είναι ίσα. Από τη μία πλευρά, το διαστημόπλοιο πρέπει να επιταχύνει έντονα όταν γυρίζει. Το σχετικό σύστημα συντεταγμένων δεν είναι συνεπώς αδρανειακό σύστημα . Επιπλέον, ένα μόνο ρολόι στο διαστημόπλοιο συγκρίνεται με πολλαπλά ρολόγια που είναι ακίνητα σε σχέση με τη Γη, δηλαδή ρολόγια στη Γη και στον προορισμό.

Με αυτή τη διευκρίνιση, είμαστε πλέον σε θέση να διατυπώσουμε με ακρίβεια τα ευρήματά μας:

διαστολή χρόνου

Ένα ρολόι U, το οποίο κινείται σε σχέση με ένα αδρανειακό σύστημα S , τρέχει πιο αργά από τα συγχρονισμένα ρολόγια στο σύστημα S σε κατάσταση ηρεμίας.

Μπορείτε να δοκιμάσετε τον βαθμό στον οποίο το τέντωμα του χρόνου επηρεάζει τις διαφορετικές ταχύτητες με μια εφαρμογή HTML5 για αυτό το θέμα.

Φυσικά, υπάρχει μια φόρμουλα για τη διαστολή του χρόνου. Έχει ως εξής:

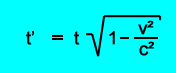
t' ... ώρα που υποδεικνύεται από το κινούμενο ρολόι U
t ... ώρα που υποδεικνύεται από τα ρολόγια του συστήματος αναφοράς S
v ... ταχύτητα του ρολογιού U σε σχέση με το πλαίσιο αναφοράς S
γ ... ταχύτητα φωτός υπό κενό

Η εφαρμογή αυτού του τύπου στην πτήση προς τα έξω ή στην επιστροφή του διαστημικού σκάφους επιβεβαιώνει το αποτέλεσμα του συλλογισμού μας χρησιμοποιώντας το διάγραμμα ts:

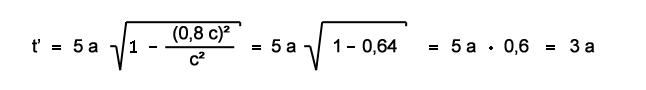
Μπορείτε να δοκιμάσετε αυτόν τον τύπο με μια μικρή αριθμομηχανή (που εφαρμόζεται ως εφαρμογή HTML5).

Όχι μόνο τα ρολόγια υπόκεινται στη διαστολή του χρόνου, αλλά γενικά όλες οι διαδικασίες, όπως η αναπνοή, ο καρδιακός παλμός, οι κινήσεις και η γήρανση. Οι αστροναύτες δεν αισθάνονται τίποτα από τη διαστολή του χρόνου στην πτήση τους στο διάστημα μέχρι να επιστρέψουν, αφού όλες οι διαδικασίες επηρεάζονται με τον ίδιο τρόπο.

Παρόλο που δικαιολογήσαμε τη χρονική διαστολή με δύο πειράματα σκέψης, μπορεί να υπάρχει μια μικρή υποψία για το αποτέλεσμα. Είμαστε πολύ συνηθισμένοι στην εσφαλμένη αντίληψη του απολύτως έγκυρου χρόνου. Επιπλέον, θα μπορούσε να γίνει κατανοητό ότι κάτι δεν πάει καλά με τα βασικά των σκέψεών μας (αρχή της σχετικότητας και σταθερότητα της ταχύτητας του φωτός). Για το λόγο αυτό, έχουν γίνει προσπάθειες να αποδειχθεί πειραματικά η διαστολή του χρόνου.

• Όταν τα σωματίδια των κοσμικών ακτίνων χτυπούν τα ανώτερα στρώματα της ατμόσφαιρας της γης, σχηματίζονται μιόνια , μεταξύ άλλων . Πρόκειται για στοιχειώδη σωματίδια που είναι παρόμοια με τα ηλεκτρόνια , αλλά έχουν πολύ μικρή μέση διάρκεια ζωής 2,2 μικροδευτερόλεπτα (2,2 εκατομμυριοστά του δευτερολέπτου) . Αν και αυτά τα μιόνια κινούνται σχεδόν με την ταχύτητα του φωτός, χωρίς χρονική διαστολή θα ταξίδευαν κατά μέσο όρο μόλις 660 m και στη συνέχεια θα διασπώνταν. Έτσι δεν θα είχαν πρακτικά καμία πιθανότητα να φτάσουν ποτέ στην επιφάνεια της γης. Στην πραγματικότητα, όμως, τα μιόνια χτυπούν τη γη σε τεράστιους αριθμούς - ως αποτέλεσμα της διαστολής του χρόνου!
• Η διαστολή του χρόνου θα μπορούσε επίσης να ελεγχθεί με πιο άμεσο τρόπο. Το 1971, οι Αμερικανοί φυσικοί Hafele και Keating πραγματοποίησαν μετρήσεις με ατομικά ρολόγια σε αεροπλάνα . Κατάφεραν να επιβεβαιώσουν τον τύπο που αναφέρθηκε παραπάνω – εντός των ορίων της ακρίβειας μέτρησης .

Στο μακρινό μέλλον, η διαστολή του χρόνου μπορεί να ανοίξει φανταστικές δυνατότητες για διαστρικές διαστημικές πτήσεις. Αλλά μια τέτοια διαστημική πτήση θα πήγαινε τους αστροναύτες στο μέλλον σαν μια χρονομηχανή (αλλά όχι προς τα πίσω!). Το αν οι αστροναύτες θα μπορούν ακόμα να βρουν το δρόμο τους όταν επιστρέψουν σε έναν πλανήτη όπου έχουν περάσει αιώνες ή χιλιετίες από τότε που έφυγαν είναι ένα άλλο ερώτημα.

ΠΗΓΉ : http://www.walter.com