Συνευθειακά σημεία & παραλληλία διανυσμάτων λυμένη άσκηση μαθηματικά β λυκείου προσανατολισμού

Λυμένες ασκήσεις στα διανύσματα Β Λυκείου – Μαθηματικά Προσανατολισμού

1.3 Συνθήκη παραλληλίας διανυσμάτων:
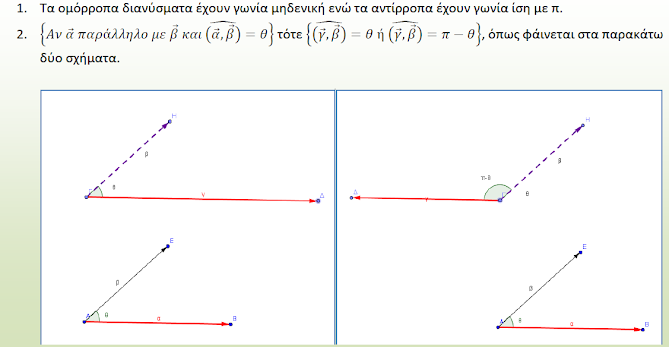
Δύο διανύσματα \( \vec{\alpha} \) και \( \vec{\beta} \) είναι παράλληλα αν και μόνο αν:
\( \vec{\alpha} = \lambda \cdot \vec{\beta} \), με \( \lambda \in \mathbb{R} \) και \( \vec{\beta} \neq \vec{0} \)
• Αν \( \lambda > 0 \) ⇒ ομόρροπα
• Αν \( \lambda < 0 \) ⇒ αντίρροπα

Άσκηση 1:

Δίνονται τα διανύσματα:
\( \vec{OA} = \vec{\alpha} + 2\vec{\beta} - 3\vec{\gamma} \),
\( \vec{OB} = 2\vec{\alpha} + \vec{\beta} + \vec{\gamma} \),
\( \vec{OG} = 4\vec{\alpha} - \vec{\beta} + 9\vec{\gamma} \)

Να δείξετε ότι τα σημεία A, B, Γ είναι συνευθειακά.

Υπολογίζουμε τα διανύσματα:
\( \vec{AB} = \vec{OB} - \vec{OA} = \vec{\alpha} - \vec{\beta} + 4\vec{\gamma} \)
\( \vec{AG} = \vec{OG} - \vec{OA} = 3\vec{\alpha} - 3\vec{\beta} + 12\vec{\gamma} \)
Παρατηρούμε ότι:
\( \vec{AG} = 3 \cdot \vec{AB} \) ⇒ τα διανύσματα είναι ομόρροπα και παράλληλα.

✅ Άρα τα σημεία A, B, Γ είναι συνευθειακά.

Άσκηση 2:

Δίνεται η ισότητα:
\( \vec{AK} + 3\vec{BK} - 2\vec{BA} = \vec{BL} + 3\vec{AM} \)

α) Να δείξετε ότι \( \vec{KL} ↑↑ \vec{MK} \)
Από την ισότητα προκύπτει:
\( 4\vec{K} = \vec{L} + 3\vec{M} \Rightarrow \vec{L} = 4\vec{K} - 3\vec{M} \)
Άρα:
\( \vec{KL} = \vec{L} - \vec{K} = 3(\vec{K} - \vec{M}) = 3\vec{MK} \)
✅ Τα διανύσματα είναι ομόρροπα ⇒ παράλληλα.

β) Τα σημεία K, Λ, M είναι συνευθειακά
Αφού \( \vec{KL} \) και \( \vec{MK} \) είναι παράλληλα ⇒ τα σημεία είναι συνευθειακά.

New Big Brain's Team

Λυμένη άσκηση με μεθοδολογία στα διανύσματα (μήκος πλευρών τριγώνου-ορθογώνιο τρίγωνο ) μαθηματικά β λυκείου προσανατολισμού

Λυμένη άσκηση στα διανύσματα Β Λυκείου, Μαθηματικά Προσανατολισμού

Δίνονται τα σημεία A(1,2), B(5,2) και Γ(1,6).
Να δείξετε ότι το τρίγωνο ΑΒΓ είναι ορθογώνιο και να προσδιορίσετε τη γωνία των 90°, χρησιμοποιώντας το Πυθαγόρειο Θεώρημα.

Βήμα 1: Υπολογισμός των μηκών των πλευρών
AB = √((5−1)² + (2−2)²) = √(16) = 4
AG = √((1−1)² + (6−2)²) = √(16) = 4
BG = √((1−5)² + (6−2)²) = √(16 + 16) = √(32)

Βήμα 2: Εφαρμογή Πυθαγορείου Θεωρήματος
AB² + AG² = BG² → 4² + 4² = (√32)² → 16 + 16 = 32
✅ Άρα το τρίγωνο είναι ορθογώνιο.

Βήμα 3: Προσδιορισμός της ορθής γωνίας
Οι πλευρές AB και AG είναι κάθετες μεταξύ τους, άρα η ορθή γωνία βρίσκεται στην κορυφή A.

Συμπέρασμα: Το τρίγωνο ABΓ είναι ορθογώνιο με ορθή γωνία στο σημείο A.

New Big Brain's Team

Διανύσματα φύλλο διαδραστικό φύλλο εργασίας στην πρόσθεση ,αφαίρεση, τον πολλαπλασιασμό αριθμού επί διάνυσμα

📘 Φύλλο Εργασίας: Διανύσματα

Άσκηση 1

Υπολόγισε: \( \vec{α} = (2,3), \vec{β} = (1,-4) \). Βρες \( \vec{α} + \vec{β} \).

Λύση: \( \vec{α} + \vec{β} = (3,-1) \)

Άσκηση 2

Υπολόγισε: \( \vec{α} = (2,3), \vec{β} = (1,-4) \). Βρες \( \vec{α} - \vec{β} \).

Λύση: \( \vec{α} - \vec{β} = (1,7) \)

Άσκηση 3

Αν \( \vec{α} = (5,-2) \), βρες \( 3 \cdot \vec{α} \).

Λύση: \( 3 \cdot \vec{α} = (15,-6) \)

Άσκηση 4

Αν \( \vec{υ} = (4,0), \vec{ν} = (-4,0) \), τι παρατηρείς;

Λύση: Έχουν ίδιο μέτρο αλλά αντίθετη κατεύθυνση → αντίθετα διανύσματα.

Άσκηση 5

Υπολόγισε: \( \vec{υ} = (7,2), \vec{ν} = (-3,5) \). Βρες \( \vec{υ} + \vec{ν} \).

Λύση: \( \vec{υ} + \vec{ν} = (4,7) \)

Άσκηση 6

Υπολόγισε: \( \vec{υ} = (7,2), \vec{ν} = (-3,5) \). Βρες \( \vec{υ} - \vec{ν} \).

Λύση: \( \vec{υ} - \vec{ν} = (10,-3) \)

Άσκηση 7

Αν \( \vec{α} = (1,2) \), βρες \( -2 \cdot \vec{α} \).

Λύση: \( -2 \cdot \vec{α} = (-2,-4) \)

Άσκηση 8

Αν \( \vec{υ} = (0,5) \), πολλαπλασίασε με 0. Τι παρατηρείς;

Λύση: \( 0 \cdot \vec{υ} = (0,0) \) → το μηδενικό διάνυσμα.

Άσκηση 9

Αν \( \vec{υ} = (3,4) \), ποιο είναι το μέτρο του;

Λύση: \( |\vec{υ}| = \sqrt{3^2+4^2} = 5 \)

Άσκηση 10

Αν \( \vec{υ} = (2,1), \vec{ν} = (4,2) \), τι σχέση έχουν;

Λύση: Είναι παράλληλα, \( \vec{ν} = 2 \cdot \vec{υ} \).

Γεωμετρική αναπαράσταση

Το διάνυσμα \( \vec{υ} = (4,3) \) σε καρτεσιανό επίπεδο.

Θεωρία μεθοδολογία και ασκήσεις στις πράξεις μεταξύ διανυσμάτων μαθηματικά προσανατολισμού β λυκείου

Πράξεις Διανυσμάτων (Β΄ Λυκείου)

Ομόρροπα Διανύσματα

\(\vec{α}=(2,0), \; \vec{β}=(3,0) \;\;\Rightarrow\;\; \vec{α}+\vec{β}=(5,0)\)

Αντίρροπα Διανύσματα

\(\vec{α}=(4,0), \; \vec{β}=(-2,0) \;\;\Rightarrow\;\; \vec{α}+\vec{β}=(2,0)\)

Κάθετα Διανύσματα

\(\vec{α}=(2,0), \; \vec{β}=(0,2) \;\;\Rightarrow\;\; \vec{α}+\vec{β}=(2,2)\)

Αφαίρεση Διανυσμάτων

\(\vec{α}=(3,2), \; \vec{β}=(1,1) \;\;\Rightarrow\;\; \vec{α}-\vec{β}=(2,1)\)

BlogThis!

Ίσα διανύσματα: κατεύθυνση και μέτρο, παραδείγματα και άσκηση μαθηματικά β λυκείου προσανατολισμού

Ίσα διανύσματα: κατεύθυνση και μέτρο, παραδείγματα και άσκηση

Με απλά λόγια και καθαρά βήματα, για μαθητές και φοιτητές.

---

Τι λέει η σχέση ισότητας διανυσμάτων

Η ακόλουθη σχέση εκφράζει τη συνθήκη για να είναι δύο διανύσματα ίσα:

\[ \vec{a} = \vec{\beta} \;\;\Leftrightarrow\;\; \vec{a} \uparrow\uparrow \vec{\beta} \;\;\text{και}\;\; |\vec{a}| = |\vec{\beta}| \]

• Ίδια κατεύθυνση: Τα διανύσματα είναι παράλληλα και δείχνουν προς την ίδια φορά.
• Ίσο μέτρο: Έχουν το ίδιο μήκος.

Με λίγα λόγια, δύο διανύσματα είναι ίσα όταν «ταυτίζονται» πλήρως ως προς κατεύθυνση και μέτρο.

---

Παράδειγμα μη ίσων διανυσμάτων

Δεδομένα: \(\vec{a} = (3,\,4)\), \(\vec{b} = \left(\tfrac{9}{5},\, \tfrac{12}{5}\right)\).

1. Έλεγχος κατεύθυνσης:
   \[ \text{Οι λόγοι } \frac{3}{\tfrac{9}{5}} \text{ και } \frac{4}{\tfrac{12}{5}} \text{ είναι ίσοι } \Rightarrow \text{παράλληλα με ίδια φορά.} \]
2. Έλεγχος μέτρων:
   \[ |\vec{a}| = \sqrt{3^2 + 4^2} = 5, \quad |\vec{b}| = \sqrt{\left(\tfrac{9}{5}\right)^2 + \left(\tfrac{12}{5}\right)^2} = 3. \]
3. Συμπέρασμα: Ίδια κατεύθυνση αλλά διαφορετικό μέτρο ⇒ δεν είναι ίσα.

Παράδειγμα ίσων διανυσμάτων

Δεδομένα: \(\vec{a} = (2,\,-1)\), \(\vec{b} = (2,\,-1)\).

1. Κατεύθυνση: Ίδιες συντεταγμένες ⇒ ίδια κατεύθυνση.
2. Μέτρο:
   \[ |\vec{a}| = |\vec{b}| = \sqrt{2^2 + (-1)^2} = \sqrt{5}. \]
3. Συμπέρασμα: \(\vec{a} = \vec{b}\).

Γεωμετρικό παράδειγμα με σημεία

Σημεία: \(A(1,2)\), \(B(4,5)\), \(C(0,0)\), \(D(3,3)\).

1. Υπολογισμός \(\vec{AB}\):
   \[ \vec{AB} = (4-1,\; 5-2) = (3,3). \]
2. Υπολογισμός \(\vec{CD}\):
   \[ \vec{CD} = (3-0,\; 3-0) = (3,3). \]
3. Συμπέρασμα: \(\vec{AB} = \vec{CD}\) παρόλο που ξεκινούν από διαφορετικά σημεία.

---

Άσκηση εξάσκησης

Δεδομένα: \(E(2,1)\), \(F(5,4)\), \(G(-1,-2)\), \(H(2,1)\).

1. Ζητούμενο 1: Βρείτε τα διανύσματα \(\vec{EF}\) και \(\vec{GH}\).
2. Ζητούμενο 2: Εξετάστε αν ισχύει \(\vec{EF} = \vec{GH}\).

Υπόδειξη: Για \(P(x_1,y_1)\), \(Q(x_2,y_2)\), έχουμε \(\vec{PQ} = (x_2 - x_1,\; y_2 - y_1)\).

Διανύσματα και βαθμωτά μεγέθη πως λειτουργούν στην καθημερινή μας ζωή

 Αναρωτηθήκατε ποτέ πώς τα αεροπλάνα πετούν στο σωστό μέρος, ακόμη και όταν ο αέρας τα σπρώχνει; Ή πώς το GPS βρίσκει την πιο γρήγορη διαδρομή προς τον προορισμό σας; Πίσω από αυτά τα ωραία πράγματα κρύβονται μερικές απλές μαθηματικές ιδέες: βαθμίδες και διανύσματα. Ας τα αναλύσουμε με τον πιο εύκολο τρόπο!

Ερωτήσεις με άμεσο έλγεχο απαντήσεων στα διανύσματα μαθηματική β λυκείου προσανατολισμού

Explore more at Quizizz.

Διανύσματα στο επίπεδο θεωρία και λυμένες ασκήσεις μαθηματικά β λυκείου

 Το αρχείο βρίσκεται εδώ

Συγγραμμικά διανύσματα συνευθειακά σημεία ασκήσεις για λύση

 

Προτεινόμενο θέμα στα διανύσματα μαθηματικά β λυκείου

 Εκφώνηση

Επιστροφή  στα   ΜΑΘΗΜΑΤΙΚΆ Β ΛΥΚΕΊΟΥ  

 

Αν θέλεις να  βλέπεις καθημερινά νέα άρθρα μπορείς να το κάνεις ακολουθώντας μας στο Facebook,  ή επισκέψου την ομάδα υποστήριξης μαθημάτων  στο Facebookκαι Instagram

Ασκήσεις στα διανύσματα μαθηματικά β λυκείου

= ΑΓ, τότε τα σημεία Α, Β, Γ είναι συνευθειακά. Σ Λ 2. _ Αν. = (- 2, 2) είναι παράλληλο με το.pdf

Ίσα διανύσματα στο παραλληλόγραμμο και νέες σχέσεις διανυσμάτων που προκύπτουν

 

Παρατηρήσεις και σχόλια μεταξύ της Ευκλείδειας γωμετρίας και της Διανυσματικής γεωμετρίας

 

Πως να υπολογίζω γραφικά την γωνία δυο διανυσμάτων, μαθηματικά β λυκείου προσανατολισμού

 

Πως αποδεικνύω ένα διάνυσμα ότι είναι μηδενικό , ίσα διανύσματα με κοινή αρχή ,ίσα διαδοχικά διανύσματα

ΕΠΙΣΤΡΟΦΗ  ΣΤΑ   

ΜΑΘΗΜΑΤΙΚΆ Β ΛΥΚΕΊΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΎ 

ΕΠΙΣΤΡΟΦΉ ΣΤΟ 

ΌΛΑ ΤΑ ΜΑΘΉΜΑΤΑ ΛΥΚΕΊΟΥ

Πρόσθεση και αφαίρεση διανυσμάτων και παραλληλόγραμμο

 

Με τι ισούται η διανυσματική ακτίνα του μέσου ενός διανύσματος ; διανύσματα β λυκείου προσανατολισμού

Έστω το διάνυσμα Ο ένα τυχαίο σημείο και Μ το μέσο του  , όπως φαίνεται στο παρακάτω σχήμα.Τότε ισχύει η σχέση

Μεθοδολογία : Πως προσθέτω δυο διανύσματα με κοινό πέρας

 Διαφορά δύο διανυσμάτων με κοινό πέρας 

Τότε αλλάζουμε την σειρά στο δεύτερο διάνυσμα, αλλάζοντας και πρόσημο σύμφωνα με την προηγούμενη παρατήρηση. Άρα προκύπτουν δύο διανύσματα διαδοχικά (κοινό πέρας με κοινή αρχή) και τα ενώνουμε.

Μεθοδολογία : Πως κάνω «Αλλαγή σειράς αρχής και πέρατος » στα διανύσματα

 

Πως προσθέτω διανύσματα ; μαθηματικά β λυκείου προσανατολισμού