Τα εξωγήινα μαθηματικά

 

Στο " The Beginning of Infinity "* Ο David Deutsch υποστηρίζει ότι ο ανθρώπινος εγκέφαλος είναι ένας λεγόμενος παγκόσμιος εξηγητής . Αυτή η δήλωση έχει πολλές διαφορετικές έννοιες, αλλά η κύρια ιδέα είναι ότι έξω από την υποκειμενική ανθρώπινη εμπειρία υπάρχει μια αντικειμενική φυσική πραγματικότητα που υπόκειται στους νόμους της φύσης και ο ανθρώπινος εγκέφαλος, χάρη στην εξέλιξη, είναι σε θέση να αναγνωρίσει και να καθορίσει οποιουσδήποτε νόμους της φύσης (άρα καθολικότητα ) μέσω του σχηματισμού φυσικών θεωριών, που εκφράζονται στη γλώσσα των μαθηματικών και επιβεβαιώνονται ή διαψεύδονται με τη βοήθεια εμπειρικών μετρήσεων.

Η δήλωση του Deutsch βρίσκεται στο σημείο τομής πολλών φιλοσοφικών ερωτημάτων και πολλά από αυτά που λέει είναι μια θέση και όχι μια σύνθεση (ή εξήγηση , όπως την αποκαλεί). ( Σημείωση σε αυτό το πλαίσιο, η διατριβή και η σύνθεση είναι μια αναφορά στην τριάδα του Χέγκελ ) Ο Deutsch σπεύδει να υπερασπιστεί την καθολικότητα της ανθρώπινης ερμηνευτικής δύναμης, συμπεριλαμβανομένης της άρνησης του ισχυρισμού του Dawkins ότι η πίεση της φυσικής επιλογής περιορίζει την ικανότητα εξήγησης.

Η ουσία της καθολικότητας του Deutsch είναι ότι οι εξηγητικές δυνάμεις του εγκεφάλου υπερβαίνουν την άμεση ανθρώπινη εμπειρία. Ακριβώς πίσω από τον πυρήνα ενός αστέρα νετρονίων, ούτε ένα άτομο ούτε κάποιο όργανο μπόρεσε να παρατηρήσει, αλλά υπάρχουν διάφορες θεωρίες σχετικά με τις διεργασίες μέσα σε τέτοια αστέρια που μπορούν να επιβεβαιωθούν ή να διαψευσθούν. Σύμφωνα με τον Deutsch, ένας λόγος για αυτό είναι ότι οι νόμοι της λογικής (οι οποίοι, τελικά, αποτελούν τη βάση των μαθηματικών) είναι άμεση συνέπεια των νόμων της φυσικής.

Αυτό είναι ένα τακτοποιημένο πνευματικό κόλπο. Εξηγεί την αδικαιολόγητη αποτελεσματικότητα των μαθηματικών στις φυσικές επιστήμες - την παρατήρηση του Eugene Wigner και άλλων ότι οι αφηρημένες μαθηματικές διαδικασίες, διαχωρισμένες από τη φυσική πραγματικότητα, είναι εξαιρετικά αποτελεσματικές στην εξήγηση του φυσικού κόσμου.

Και ναι, τα μαθηματικά είναι πράγματι συχνά αποτελεσματικά, αλλά όχι πάντα. Μπορεί κανείς να φανταστεί οποιαδήποτε φανταστικά φαινόμενα που ταιριάζουν σε μια τέτοια περιγραφή, για παράδειγμα, μαύρη ύλη. Αλλά δεν χρειάζεται να μπει κανείς σε μια τέτοια ζούγκλα για να βρει προβληματικές περιοχές στην ικανότητά μας να εξηγούμε τα πράγματα.

Η συμπεριφορά κάποιων απλών φυσικών συστημάτων αψηφούσε την εξήγηση για αιώνες.

Η πολυχρηστικότητα καταρρέει

Τα φυσικά μοντέλα είναι πολύ κατάλληλα για να εξηγήσουν γραμμικά φαινόμενα. Σε γενικές γραμμές, γραμμικά φαινόμενα είναι εκείνα τα φαινόμενα που μπορούν να εκφραστούν σε γραμμικά συστήματα εξισώσεων. Οι ίδιες οι εξισώσεις μπορεί να είναι διαφορικές, που περιγράφουν δυναμικές διεργασίες, στοχαστικές, εκφράζοντας πιθανότητες ή οποιαδήποτε άλλη γραμμική μορφή.

Πολλές φυσικές διεργασίες, όπως το πρόβλημα των δύο σωμάτων, η μεταφορά θερμότητας, τα μοντέλα ιδανικών αερίων και άλλες, μπορούν είτε να εκφραστούν ακριβώς ως γραμμικά συστήματα είτε να προσεγγιστούν πολύ καλά με αυτά τα συστήματα. Μερικά μη γραμμικά φαινόμενα μπορούν να μοντελοποιηθούν με ακρίβεια υποθέτοντας την τοπική γραμμικότητα και σχηματίζοντας ένα σύστημα μικροσκοπικών γραμμικών βημάτων, προσαρμόζοντάς τα καθώς προχωράτε.

Αλλά, δυστυχώς, πολλά (στην πραγματικότητα τα περισσότερα) πραγματικά φυσικά φαινόμενα δεν είναι μόνο μη γραμμικής φύσης, αλλά επίσης δεν μπορούν να προσεγγιστούν αρκετά καλά ως γραμμικά συστήματα. Τα τρία πιο γνωστά παραδείγματα τέτοιων φαινομένων είναι το πρόβλημα της βαρύτητας του σώματος Ν, οι αναταράξεις και, το προσωπικό μου αγαπημένο, το διπλό εκκρεμές.

Σε καθένα από αυτά τα παραδείγματα, το πρόβλημα δεν είναι η έλλειψη ενός μαθηματικού μοντέλου που να περιγράφει το ίδιο το φαινόμενο. Στην πραγματικότητα, αυτά τα μοντέλα είναι αρκετά απλά. Η δυναμική ενός διπλού εκκρεμούς, δηλαδή οι εξισώσεις που καθορίζουν με ακρίβεια τη θέση του στο χώρο κάθε δεδομένη στιγμή, παρουσιάζονται παρακάτω:

Κέντρο του πρώτου εκκρεμούς

Το κέντρο του δεύτερου εκκρεμούς

Έτσι, η κίνηση του εκκρεμούς στο χώρο καθορίζεται επίσης από αυτές τις εξισώσεις. Όμως, παρά την ικανότητα ακριβούς προσδιορισμού της θέσης του εκκρεμούς, είναι αδύνατο να υπολογιστεί η χρονική εξέλιξη αυτού του δυναμικού συστήματος. Με άλλα λόγια, δεν υπάρχει τέτοια εξίσωση (για την οποία γνωρίζουμε) που θα μας επέτρεπε να γνωρίζουμε με ακρίβεια τη θέση του εκκρεμούς μετά από κάποιο χρονικό διάστημα, λαμβάνοντας υπόψη την τρέχουσα θέση του.

Αλλά στην πραγματικότητα το πρόβλημα είναι ακόμη χειρότερο, αφού δεν μπορούμε να προσεγγίσουμε καλά αυτό το σύστημα. Το διπλό εκκρεμές έχει την εξής ιδιότητα: μικρές αλλαγές στις αρχικές συνθήκες οδηγούν σε μεγάλες αλλαγές στο τελικό αποτέλεσμα. Επομένως, μικρές ανακρίβειες στην προσέγγιση οδηγούν σε απόκλιση του συστήματος**. Για παράδειγμα, για να αυξηθεί η ακρίβεια κατά ένα ψηφίο, είναι απαραίτητο να αυξηθεί ο αριθμός των βημάτων προσέγγισης κατά τάξη μεγέθους, δηλ. χρήση υπολογιστή.  

Πρέπει να επαναλάβουμε ότι οι εξισώσεις είναι ακριβείς. Κανένας εξωτερικός φυσικός παράγοντας δεν απαιτείται για να εξηγήσει τον λόγο της αδυναμίας πρόβλεψης της δυναμικής του εκκρεμούς - αυτό είναι μια ιδιότητα των ίδιων των εξισώσεων που διέπουν, και όχι η τύχη, η κβαντική φυσική ή κάτι άλλο.

Με φόντο τον βαθμό στον οποίο τα φυσικά μοντέλα μας επιτρέπουν να εξηγήσουμε(και επομένως να κάνουμε προβλέψεις) η πραγματικότητα, η αδυναμία πρόβλεψης της κατάστασης ενός απλού συστήματος σε αυθαίρετους χρόνους με άπειρη ακρίβεια, φαίνεται να δείχνει ότι τα μαθηματικά μας δεν είναι καθολικά.

Αυτή η περίεργη δυαδικότητα με έχει εκπλήξει από τότε που σπούδασα μαθηματικά.

Αποδεικνύεται ότι μπορούμε να περιγράψουμε με ακρίβεια διάφορα φαινόμενα με πολύ απλά συστήματα, αλλά μερικές φορές είναι απλά αδύνατο να τα χρησιμοποιήσουμε για να προβλέψουμε τα επιθυμητά φαινόμενα; Σε αντίθεση με την έλλειψη πληροφοριών για την περιγραφή των φυσικών διεργασιών, αυτό είναι ένα εντελώς διαφορετικό πρόβλημα - όλες οι πληροφορίες είναι διαθέσιμες, αλλά φαίνεται ότι υπάρχει κάποιο αόρατο εμπόδιο.

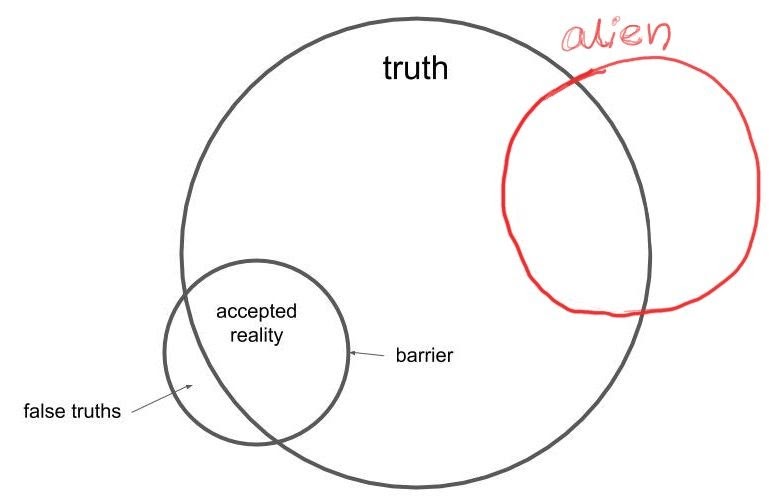
Υπάρχουν κενά στη βάση των μαθηματικών μας; Το πρόβλημα βρίσκεται στην ίδια τη λογική, που βάζει μια ακτίνα στον τροχό της επεξηγηματικής ικανότητας του ανθρώπου; Αυτά τα κενά οφείλονται σε κάποιο περιορισμό της ανθρώπινης αντίληψης; Υπάρχουν άλλα φαινόμενα που ξεπερνούν το φράγμα αυτών των περιορισμών;

Εξωγήινα μαθηματικά πίσω από το φράγμα

Στο Fire in the sky, ο Mike Solana υποστηρίζει ότι το φαινόμενο των θεατών UFO πρέπει να ληφθεί σοβαρά υπόψη, επειδή ένα τέτοιο γεγονός θα είχε απίστευτη σημασία, ανεξάρτητα από τα αίτια του (κυβερνητική κάλυψη, εξωγήινοι, ταξίδια στο χρόνο ...). Το ορίζει ως εμπόδιο της πίστης: οι άνθρωποι δεν φαίνεται να μπορούν να πάρουν στα σοβαρά τέτοια φαινόμενα.

Επιπλέον, ο Solana σημειώνει ένα άλλο ενδιαφέρον σημείο - τέτοια φαινόμενα μπορεί να είναι τόσο πολύ πέρα ​​από τα όρια της ανθρώπινης εμπειρίας που η γνωστική-αισθητηριακή συσκευή ενός ατόμου δεν μπορεί να τα καταλάβει. Αντιληπτικό ή γνωστικό εμπόδιο.

Όπως δείξαμε με το παράδειγμα του διπλού εκκρεμούς, αυτή δεν είναι μια τραβηγμένη ιδέα. Τέτοια εμπόδια συμβαίνουν στα δικά μας μαθηματικά. Αυτά τα πράγματα συνεπάγονται θεμελιώδεις περιορισμούς στο τι μπορούμε ποτέ να εξηγήσουμε;

Ας υποθέσουμε για λίγο ότι ο Deutsch έχει δίκιο για την αντικειμενική φυσική πραγματικότητα και ο Solana έχει δίκιο για τους περιορισμούς της ανθρώπινης αντίληψης και γνώσης. Ας υποθέσουμε επίσης ότι αυτοί οι περιορισμοί δεν επιτρέπουν καν να σκεφτόμαστε φαινόμενα εκτός του φραγμού. ότι η αδυναμία μας να προβλέψουμε τη συμπεριφορά του διπλού εκκρεμούς είναι αποτέλεσμα του περιβάλλοντος στο οποίο αναπτύξαμε. ότι τα φαινόμενα που διαμόρφωσαν την αφηρημένη σκέψη στους πρώτους ανθρώπους ήταν γραμμικά.

Τι γίνεται με τα αισθανόμενα είδη που εξελίχθηκαν υπό άλλες συνθήκες; ***

Αντιμέτωποι με μια μη γραμμική φυσική πραγματικότητα, προκειμένου να επιτύχει ένα ορισμένο επίπεδο επεξηγηματικής δύναμης, τα εξωγήινα μαθηματικά θα πρέπει να αντιμετωπίσουν τη μη γραμμικότητα ως βασική ιδιότητα, ακριβώς την ίδια με τη γραμμικότητα και τα απειροελάχιστα στη δική μας. Θα μπορούσαν να εξηγήσουν και, επομένως, να αξιοποιήσουν και να προβλέψουν ένα εντελώς διαφορετικό, ίσως ευρύτερο φάσμα φυσικών φαινομένων από εμάς. Είναι πολύ πιθανό οι συνέπειες αυτών των ανακαλύψεων να είναι ακατανόητες για τη δική μας επεξηγηματική συσκευή.

Τα εξωγήινα μαθηματικά θα είχαν διαφορετική ερμηνευτική δύναμη. Έχοντας ένα διαφορετικό γνωστικό εμπόδιο, και θα μπορούσαν να έχουν μεγάλα προβλήματα να αντιληφθούν το μέρος της πραγματικότητας στο οποίο βρισκόμαστε. Η επικοινωνία μας μαζί τους θα ήταν στην καλύτερη περίπτωση δύσκολη.

Αυτές οι ιδέες δεν έρχονται σε αντίθεση ούτε με τον Ντόιτς ούτε τον Σολάνα. Διατηρούν την ιδέα μιας αντικειμενικής φυσικής πραγματικότητας στην οποία τόσο εμείς οι άνθρωποι όσο και οι εξωγήινοι αλληλεπιδρούμε μέσω φυσικών φαινομένων και αυτή η πραγματικότητα μπορεί να εξηγηθεί χωρίς να αρνηθεί κανείς την πιθανότητα ύπαρξης φαινομένων πέρα ​​από τα όρια των ανθρώπινων ικανοτήτων κατανόησης.

Η Deutsch μπορεί να έχει δίκιο ότι η λογική είναι συνέπεια φυσικών νόμων. αλλά η ανθρωπότητα δεν έλαβε όλους τους νόμους του σύμπαντος με την απόκτηση της συνείδησης. Και μην υποθέσετε ότι η λογική μας είναι απόλυτη. Ίσως κάποιος άλλος κατέληξε σε διαφορετική λογική λόγω της ανάγκης να εξηγήσει εντελώς διαφορετικά φαινόμενα.

Όπως και να έχει, αναζητώντας το εμπόδιο και τα πράγματα πέρα ​​από αυτό, παραδεχόμαστε τουλάχιστον τη δυνατότητα να επεκτείνουμε το εύρος των πραγμάτων που μπορεί να σκεφτεί κάποιος και, τελικά, τη βάση της επεξηγηματικής μας δύναμης. Ίσως αν συναντήσουμε ένα είδος με εξωγήινα μη γραμμικά μαθηματικά, μπορούμε να βρούμε έναν τρόπο να μοιραστούμε τις γνώσεις μας και να συνθέσουμε πιο καθολική λογική στην προσπάθειά μας να γίνουμε καθολικοί εξηγητές.

Αλλά αν δεν μοιραστούν τη γνώση τους μαζί μας ή αν δεν τους συναντήσουμε ποτέ, τότε μέσω της αποφασιστικής μας παρατήρησης και της θεμελιώδης ανθρώπινης ανάγκης για κατανόηση, ίσως μπορούμε να το χειριστούμε μόνοι μας.

ΥΓ:

Αφού μίλησα με τον Μάικ Σολάνα, κατέληξα σε ένα ελαφρώς διαφορετικό σενάριο. Αν υποθέσουμε ότι η ανθρώπινη γνώση (η διαδικασία παραγωγής εξηγήσεων) μπορεί να μιμηθεί **** από μια μηχανή Turing (κάτι που κάνουν συχνά ο Deutsch και άλλοι συγγραφείς), τότε χρειάζεται μόνο να βρούμε ένα φαινόμενο στην αντικειμενική πραγματικότητα που δεν είναι μόνο υπολογιστικά αναποφάσιστο από μια κλασική μηχανή Turing, αλλά η εξήγηση του οποίου είναι ακατανόητη.

Σε αυτό το σενάριο, έχουμε πραγματικά μεγάλα προβλήματα με το τι θα μπορέσουμε ποτέ να εξηγήσουμε. Σφραγισμένο έξυπνο κουτί που δεν μπορεί να σπάσει φυσικά.

Αυτή είναι μια σκέψη κοσμικού επιπέδου τρόμου και μάλλον θα το σκεφτώ στο μέλλον.


* Έχω μια δύσκολη σχέση με το The Beginning of Infinity . Από τη μια πλευρά, η Deutsch κάνει συνεχώς ισχυρισμούς ότι ξέρω ότι δεν είναι αληθινές (όπως η δυνατότητα υπολογισμού), κάτι που κάνει το βιβλίο στο σύνολό του μάλλον αμφισβητήσιμο, και από την άλλη, η ανάγνωση με κάνει να σκέφτομαι πράγματα που προηγουμένως και δεν υποψιαζόμουν . Παραδόξως, η Deutsch λέει την αλήθειαδηλώσεις σε επιστημονικά άρθρα τους για τα ίδια θέματα (ακριβέστερα, για τη φυσική και τη θεωρία της υπολογισιμότητας).

** Μια επίσημη ποσοτική εκτίμηση του πόσο γρήγορα αποκλίνουν οι τροχιές ενός δυναμικού συστήματος με την πάροδο του χρόνου ονομάζεται χρόνος Lyapunov . Ρώσοι και σοβιετικοί μαθηματικοί, ιδιαίτερα ο Lyapunov , ο Kolmogorov και πολλοί άλλοι, έκαναν θεμελιώδη εργασία σε αυτόν τον τομέα.

*** Στο " The Three-Body Problem "Οι ακόλουθες συνθήκες σημειώνονται εύστοχα: ένα εξωγήινο είδος εξελίσσεται σε ένα περιβάλλον με ιδιότητες πολύ παρόμοιες με ένα διπλό εκκρεμές. ζουν σε έναν πλανήτη που περιστρέφεται γύρω από ένα σύστημα τριών αστέρων. Αναγκάζονται πολύ νωρίτερα να αναπτύξουν ξένα για εμάς μη γραμμικά μαθηματικά, τα οποία θα οδηγήσουν σε μεγάλα τεχνολογικά πλεονεκτήματα. Αλλά η αφηρημένη σκέψη τους δεν έχει το βάθος των επικοινωνιακών ικανοτήτων των ανθρώπων - δεν μπορούν να πουν ψέματα ή καν να φανταστούν ένα ψέμα.

**** Η εξομοίωση έχει αυστηρό μαθηματικό ορισμό. μια μηχανή κατάστασης μιμείται μια άλλη εάν μπορεί να επιτύχει την ίδια ακολουθία εξόδου με την ίδια ακολουθία εισόδου.