Ο κόσμος των Παράδοξων μαθηματικών

Σήμερα θα ήθελα να θίξω ένα τόσο συναρπαστικό θέμα όπως τα μαθηματικά παράδοξα. 

The Heap Paradox και το Bald Paradox

Αυτά τα παράδοξα ήταν γνωστά από την αρχαιότητα. Αρχικά, ας διατυπώσουμε και ας εξετάσουμε το παράδοξο ενός σωρού που σχετίζεται με την αβεβαιότητα της έννοιας του «σωρού»:

«αν ένας κόκκος προστεθεί σε έναν κόκκο, τότε σε ποια στιγμή σχηματίζεται ένας σωρός;»
ή η αντίστροφη διατύπωση:
"αφαιρώντας έναν κόκκο από ένα σωρό 1 εκατομμυρίου κόκκων, από ποια στιγμή παύει να είναι σωρός;"

Η διατύπωση του παραδόξου βασίζεται στην προφανή υπόθεση ότι ένας σπόρος δεν σχηματίζει σωρό και στην επαγωγική προϋπόθεση ότι η προσθήκη ενός σπόρου σε μια συλλογή που δεν είναι σωρός δεν είναι απαραίτητη για το σχηματισμό ενός σωρού. Από αυτές τις προϋποθέσεις προκύπτει ότι καμία συλλογή αυθαίρετα μεγάλου αριθμού κόκκων δεν θα σχηματίσει σωρούς, γεγονός που έρχεται σε αντίθεση με την ιδέα της ύπαρξης ενός σωρού κόκκων. Προφανώς, αυτά τα επιχειρήματα οδηγούν σε λάθος συμπεράσματα.

Ωστόσο, μέχρι πολύ πρόσφατα δεν ήταν σαφές ποιο σκεπτικό να χρησιμοποιήσω εδώ. Μόνο με την εμφάνιση της θεωρίας των ασαφών συνόλων και της ασαφούς λογικής του Lofty Zadeh, κατέστη σαφές ότι ο ασαφής συλλογισμός είναι κατάλληλος εδώ, αφού υπάρχει ένα κλασικό αντικείμενο ασαφούς λογικής - η αόριστη έννοια του "να είσαι σωρός". Αυτά τα αντικείμενα στη ασαφή λογική ερμηνεύονται ότι έχουν μια ανακριβή τιμή που χαρακτηρίζεται από κάποιο ασαφές σύνολο.

Σύμφωνα με αυτό το σκεπτικό, το συμπέρασμα σε κάθε βήμα παραμένει το ίδιο, αλλά η συμμετοχή της ορθότητάς του μειώνεται με κάθε βήμα. Όταν αυτό το ανήκειν πέσει κάτω από το 50%, τότε το αντίθετο συμπέρασμα γίνεται πιο σωστό.

Παρόμοιος συλλογισμός μπορεί να εφαρμοστεί στο παράδοξο «Φαλακρό»:
«Αν οι τρίχες πέφτουν από το κεφάλι μία κάθε φορά, σε ποιο σημείο γίνεται φαλακρός ένας άνθρωπος;»

Ψεύτης παράδοξο

Εάν η δήλωση στην εικόνα είναι αληθής, τότε, με βάση το περιεχόμενό της, είναι αλήθεια ότι είναι ψευδής. αλλά αν είναι ψευδές, τότε αυτό που λέει είναι ψευδές. Ως εκ τούτου, δεν είναι αλήθεια ότι η δήλωση στην εικόνα είναι ψευδής, και ως εκ τούτου η δήλωση είναι αληθής.

Το παράδοξο του ψεύτη καταδεικνύει την απόκλιση της καθομιλουμένης από την τυπική λογική εισάγοντας μια πρόταση που είναι και αληθινή και ψευδής. Στο πλαίσιο της τυπικής λογικής, αυτή η δήλωση δεν είναι αποδείξιμη και αδιάψευστη, επομένως, δεν υπάρχει λύση σε αυτό το παράδοξο, αλλά υπάρχουν διάφορες επιλογές για την εξάλειψή του.

Για να γίνει αυτό, μπορούμε να εφαρμόσουμε τη συλλογιστική που χρησιμοποιήθηκε στην προηγούμενη ενότητα, γι' αυτό υποθέτουμε ότι η πρόταση είναι αληθής κατά 0,5, τότε είναι ψευδής κατά 0,5, δηλαδή, δεν μπορεί να ονομαστεί κάθε φράση εντελώς ψευδής ή εντελώς σωστή - " κατά κάποιο τρόπο η δήλωση στην εικόνα λέει ψέματα, αλλά σε κάτι λέει την αλήθεια.»

Το ίδιο συμπέρασμα μπορεί να εξαχθεί χρησιμοποιώντας τριμερή λογική. Έχει τρεις βαθμούς αλήθειας: «αληθής», «ψευδής» και «αόριστον». Με τον όρο «επ' αόριστον» εννοείται μια ενδιάμεση έννοια μεταξύ αληθινού και ψευδούς. Το παράδοξο του ψεύτη αναφέρεται σε αυτόν τον βαθμό αλήθειας.

Όπως ήδη αναφέρθηκε, αυτές δεν είναι λύσεις στο παράδοξο του ψεύτη, αλλά μόνο εξηγήσεις γιατί αυτό το παράδοξο προκύπτει στην κλασική προτασιακή λογική δύο αξιών. Καταθέτουν ότι ο αυστηρός διαχωρισμός όλων των δηλώσεων σε αληθές και ψευδείς δεν μπορεί να εφαρμοστεί σε αυτή την περίπτωση, καθώς οδηγεί σε ένα παράδοξο.

Επί του παρόντος, πολλοί εμμένουν στην άποψη ότι αυτή η δήλωση δεν είναι καθόλου λογική δήλωση και είναι άσκοπο να εφαρμόζουμε τις κλασικές μεθόδους τυπικής λογικής σε αυτήν.

Το παράδοξο του Θησέα

Αυτό το παράδοξο μπορεί να διατυπωθεί ως εξής:

"Εάν όλα τα συστατικά μέρη του αρχικού αντικειμένου αντικαταστάθηκαν, το αντικείμενο παραμένει το ίδιο αντικείμενο;"

Έχουν προταθεί αρκετές λύσεις σε αυτό το παράδοξο. Σύμφωνα με τη φιλοσοφική σχολή του Αριστοτέλη, υπάρχουν διάφοροι λόγοι που περιγράφουν ένα αντικείμενο: η μορφή, το υλικό και η ουσία του πράγματος (που, σύμφωνα με τον Αριστοτέλη, είναι το πιο σημαντικό χαρακτηριστικό). Με βάση αυτό, το πλοίο παρέμεινε το ίδιο, αφού η ουσία του δεν έχει αλλάξει, μόνο το φθαρμένο υλικό έχει αλλάξει.

Στην επόμενη απόφαση προτάθηκε να δοθεί στο επιχείρημα «το ίδιο» ποσοτικό και ποιοτικό χαρακτηριστικό. Σε αυτή την περίπτωση, μετά την αλλαγή των σανίδων, το πλοίο του Θησέα θα αποδειχθεί ποσοτικά το ίδιο, αλλά ποιοτικά - ήδη ένα διαφορετικό πλοίο.

Πρόσφατα, για να λυθεί το παράδοξο του Θησέα, έχει προταθεί η χρήση μιας 4-διάστατης ερμηνείας, στην οποία το τρισδιάστατο πλοίο έχει επίσης επέκταση στον 4-διάστατο χρόνο. Το προκύπτον 4-διάστατο πλοίο είναι ποσοτικά πανομοιότυπο με τον εαυτό του σε όλη τη χρονοσειρά. Αλλά τα μεμονωμένα "χρονικά κομμάτια" μπορούν να διαφέρουν ποιοτικά μεταξύ τους.

Abilene παράδοξο

Αυτό το παράδοξο έγκειται στο γεγονός ότι μια ομάδα ανθρώπων μπορεί να πάρει μια απόφαση που έρχεται σε αντίθεση με την πιθανή επιλογή οποιουδήποτε από τα μέλη της ομάδας, λόγω του γεγονότος ότι κάθε άτομο πιστεύει ότι οι στόχοι του είναι αντίθετοι με τους στόχους της ομάδας, και επομένως δεν πειράζει.

Το παράδοξο περιγράφηκε από τον Jerry Harvey στο The Abilene Paradox and other Meditations on Management. Το όνομα του παραδόξου δίνεται με βάση το ακόλουθο ανέκδοτο που περιγράφεται σε αυτό το άρθρο:

Ένα ζεστό βράδυ του Τέξας, μια συγκεκριμένη οικογένεια έπαιζε ντόμινο στη βεράντα μέχρι που ο πεθερός τους πρότεινε να πάνε στην Άμπιλεν για δείπνο. Η σύζυγος είπε: «Καλό ακούγεται». Ο σύζυγος, παρά το γεγονός ότι το ταξίδι υποσχέθηκε να είναι μακρύ και ζεστό, σκέφτηκε ότι θα ήταν απαραίτητο να προσαρμοστεί στους άλλους και είπε: «Νομίζω ότι δεν είναι κακό. Ελπίζω να μην πειράζει η μαμά σου». Η πεθερά απάντησε: «Φυσικά, πάμε! Δεν έχω πάει στο Abilene για πολύ καιρό».
Ο δρόμος ήταν ζεστός, σκονισμένος και μακρύς. Όταν τελικά έφτασαν στην καφετέρια, το φαγητό ήταν άγευστο. Τέσσερις ώρες αργότερα, εξαντλημένοι, επέστρεψαν σπίτι.

Ένας από αυτούς είπε ανειλικρινά: «Δεν ήταν κακό ταξίδι, σωστά;» Η πεθερά είπε σε αυτό ότι, μάλιστα, θα ήταν καλύτερα να μείνει στο σπίτι, αλλά πήγε, αφού οι άλλες τρεις ήταν γεμάτες ενθουσιασμό. Ο σύζυγος είπε: «Θα χαιρόμουν να μην πάω πουθενά, πήγα μόνο για να ευχαριστήσω τους άλλους». Η σύζυγος είπε: «Και πήγα, υπολογίζοντας στη χαρά των άλλων. Έπρεπε να είσαι τρελός για να γίνεις εθελοντής σε αυτό το ταξίδι». Ο πεθερός απάντησε ότι το πρότεινε μόνο επειδή νόμιζε ότι οι άλλοι βαριόνταν.

Και κάθισαν εκεί, άναυδοι που είχαν πάει ένα ταξίδι που κανένας τους δεν ήθελε. Καθένας από αυτούς θα προτιμούσε να απολαύσει εκείνη τη μέρα με την ησυχία του.

Αυτό το παράδοξο εξηγείται εύκολα από διάφορες κοινωνιολογικές επιστήμες, οι οποίες επιβεβαιώνουν ότι ένα άτομο σπάνια εκτελεί ενέργειες που έρχονται σε αντίθεση με τις ενέργειες της ομάδας του. Νομίζω ότι πολλοί άνθρωποι έχουν συναντήσει αυτό το παράδοξο περισσότερες από μία φορές στη ζωή τους.

Το παράδοξο Simpson και το φαινόμενο Will Rogers

Σημειώνω ότι αυτά τα παράδοξα είναι «φαινομενικά», δηλαδή μπορούν να προκύψουν σε διαισθητικό επίπεδο, αλλά αν κάνετε υπολογισμούς, είναι εύκολο να βεβαιωθείτε ότι δεν θα προκύψει παράδοξο.

Για να δείξετε το παράδοξο του Simpson, εξετάστε ένα παράδειγμα που περιγράφεται από τον διάσημο εκλαϊκευτή των μαθηματικών Martin Gardner .

Ας υποθέσουμε ότι έχουμε τέσσερα σετ πέτρες. Η πιθανότητα να τραβήξετε μια μαύρη πέτρα από το σετ Νο. 1 είναι μεγαλύτερη από ό,τι από το σετ Νο. 2. Με τη σειρά της, η πιθανότητα να τραβήξετε μια μαύρη πέτρα από το σετ Νο. 3 είναι μεγαλύτερη από ό,τι από το σετ Νο. 4. Ας συνδυάσουμε το σετ Νο. 1 με σετ Νο. 3 (λαμβάνουμε σετ Ι) και σετ Νο. 2 - με σετ Νο. 4 (σετ ΙΙ). Διαισθητικά, θα περίμενε κανείς ότι η πιθανότητα να τραβήξει κανείς μια μαύρη πέτρα από το σύνολο I θα ήταν μεγαλύτερη από ό,τι από το σύνολο II. Ωστόσο, αυτή η δήλωση δεν είναι αλήθεια γενικά.

Ένα παράδειγμα όπου ισχύει το παράδοξο του Simpson:

	μαύρες μπάλες	λευκές μπάλες	Πιθανότητα σχεδίασης μαύρης πέτρας
Σετ #1	6	7	6/13 ≈ 0,4615
Σετ #2	4	5	4/9 ≈ 0,4444
Σετ #3	6	3	6/9 ≈ 0,6667
Σετ #4	9	5	9/14 ≈ 0,6429

Τώρα ας αναμίξουμε τα σετ #1 και #3 — από τα οποία μπορούν να σχεδιαστούν μαύρες πέτρες με μεγαλύτερη πιθανότητα, και σετ #2 και #4 — από τα οποία μπορούν να σχεδιαστούν μαύρες πέτρες με λιγότερες πιθανότητες.

	μαύρες μπάλες	λευκές μπάλες	Πιθανότητα σχεδίασης μαύρης πέτρας
Σετ Ι	12	10	12/22 ≈ 0,5454
Σετ II	13	10	13/23 ≈ 0,5652

Όπως μπορούμε να δούμε από τον πίνακα, μετά την ανάμειξη, η πιθανότητα να τραβηχτεί μια μαύρη πέτρα από το σύνολο ΙΙ έγινε μεγαλύτερη από ό,τι από το σύνολο Ι. Μαθηματικά,

δεν υπάρχει παράδοξο εδώ, αφού η συνολική πιθανότητα ενός συνόλου εξαρτάται από την αναλογία του αριθμού από μαύρες πέτρες και τα δύο χρώματα, σε αυτήν την περίπτωση, στο σετ 4 ήταν 9 μαύρες πέτρες, και στο πρώτο υπάρχουν ήδη 7 λευκές, που περισσότερο από όλα επηρέασαν την τελική ευθυγράμμιση.

Κοντά στο παράδοξο Simpson και το φαινόμενο του Will Rogers. Στην πραγματικότητα, περιγράφουν το ίδιο φαινόμενο, αλλά με διαφορετικούς όρους.
Νομίζω ότι πολλοί άνθρωποι έχουν συναντήσει φράσεις όπως αυτή περισσότερες από μία φορές:
"Όταν οι Okies άφησαν την Οκλαχόμα και μετακόμισαν στην Καλιφόρνια, αύξησαν τη μέση νοημοσύνη και των δύο πολιτειών."

Αυτή η φράση αποδίδεται στον Will Rogers, από τον οποίο το φαινόμενο πήρε το όνομά του .

Από τη σκοπιά των μαθηματικών, ούτε εδώ υπάρχει παράδοξο. Για να το επαληθεύσουμε αυτό, αρκεί να εξετάσουμε δύο σύνολα: το πρώτο είναι {1, 2} και το δεύτερο είναι {90.100}, εάν ο αριθμός 90 από το δεύτερο σύνολο μεταφερθεί στο πρώτο, τότε ο αριθμητικός μέσος όρος των στοιχείων τόσο του πρώτου σετ όσο και του δεύτερου θα αυξηθούν.

Εξαφάνιση κυττάρων

Μια ευρεία κατηγορία προβλημάτων σχετικά με τη μετάθεση μορφών που έχουν σημάδια σοφισμού: αρχικά, εισήχθη ένα συγκαλυμμένο σφάλμα στην κατάστασή τους. Σε κάποιο βαθμό, αυτά τα προβλήματα είναι πιο κοντά στις οπτικές ψευδαισθήσεις παρά στα μαθηματικά.

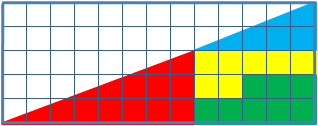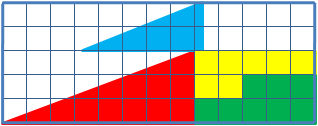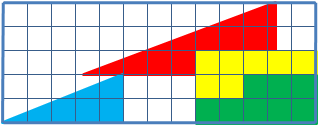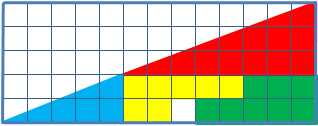
Για παράδειγμα, εξετάστε ένα παρόμοιο πρόβλημα: δίνεται ένα ορθογώνιο τρίγωνο 13×5 κελιά, που αποτελείται από 4 μέρη. Μετά την αναδιάταξη των εξαρτημάτων διατηρώντας οπτικά τις αρχικές αναλογίες, εμφανίζεται ένα επιπλέον κελί, που δεν καταλαμβάνεται από κανένα εξάρτημα.

Μαθηματικά, δεν υπάρχουν παράδοξα και η μυστηριώδης εξαφάνιση της πλατείας. Τα οπτικά παρατηρούμενα τρίγωνα, στην πραγματικότητα, δεν είναι, οι υποτείνουσες και στα δύο ψευδότριγωνα είναι στην πραγματικότητα διακεκομμένες γραμμές (στο πρώτο τρίγωνο είναι με διάλειμμα προς τα μέσα και στο δεύτερο - προς τα έξω). Εάν ένα τρίγωνο υπερτίθεται το ένα πάνω στο άλλο, τότε σχηματίζεται ένα παραλληλόγραμμο μεταξύ των «υποτένυσών» τους, το οποίο περιέχει την περιοχή «που λείπει».

Αντί για συμπέρασμα

Προς μεγάλη μου λύπη, είναι αδύνατο να εξεταστούν όλα τα ενδιαφέροντα μαθηματικά παράδοξα (και «όχι αρκετά» παράδοξα) στο πλαίσιο ενός άρθρου. Ελπίζω όμως αυτό το άρθρο να μην σας άφησε αδιάφορους και θα χαρώ πολύ αν αποφασίσετε ότι δεν χάσατε το χρόνο σας διαβάζοντας μάταια