Μερικοί άνθρωποι συνδέουν τη λέξη "μαθηματικά" με την αιώνια στοιβασία και έναν αυστηρό δάσκαλο, ενώ άλλοι φαντάζονται κάποιο είδος αφαίρεσης που υπάρχει ξεχωριστά από τον κόσμο μας, αλλά υπάρχουν και εκείνοι που βλέπουν τις εκδηλώσεις αυτής της επιστήμης στην καθημερινή μας ζωή.
Για παράδειγμα, ξέρετε ότι το σχήμα των δοντιών στα γρανάζια στα συνηθισμένα ρολόγια έχει πολύ πιο περίπλοκο σχήμα από ένα τραπεζοειδές και ονομάζεται η μαγική λέξη "κύκλος involute"; Είναι ίσως η πρώτη φορά που το ακούτε, αν και όλοι είναι εξοικειωμένοι τόσο με τα μηχανικά ρολόγια όσο και με τα γρανάζια. Το ερώτημα γιατί επιλέχθηκε αυτή η φόρμα, θα εξετάσουμε ξεχωριστά αργότερα. Γιατί όμως τόσοι πολλοί άνθρωποι πιστεύουν ότι τα μαθηματικά είναι κάτι βαρετό και κουραστικό; Αυτό οφείλεται πρωτίστως στο γεγονός ότι στα περισσότερα σχολεία δίνουν μόνο «βάση» -βασικές μαθηματικές έννοιες- χωρίς αναφορά στην πραγματική ζωή. Το υλικό που λαμβάνεται με αυτόν τον τρόπο φαίνεται στεγνό και βαρετό. «Λοιπόν, πού μπορώ να συναντήσω αυτές τις τριγωνομετρικές εξισώσεις στη ζωή μου;» - ένα τέτοιο άτομο εκπλήσσεται. Αλλά αξίζει να ρίξετε μια πιο προσεκτική ματιά και θα ανοίξει ένας εκπληκτικός, αστραφτερός κόσμος,
Για να είμαστε δίκαιοι, πρέπει να ειπωθεί ότι - ναι, δεν εφαρμόζονται πλέον όλες οι μαθηματικές ανακαλύψεις και μέθοδοι, αλλά είναι ήδη έτοιμες για χρήση και απλώς περιμένουν στα φτερά.
Θα ήθελα να μιλήσω για μια τέτοια περίπτωση. Ο συμπατριώτης μας, ο μεγάλος μαθηματικός Νικολάι Ιβάνοβιτς Λομπατσέφσκι, πρύτανης του Πανεπιστημίου του Καζάν το 1827-1846, που έζησε τον 19ο αιώνα, ανέπτυξε επιμελώς για πολλά χρόνια μια νέα, μη ευκλείδεια γεωμετρία. Ωστόσο, μετά τη δημοσίευση των έργων του το 1832, επικρίθηκε αυστηρά και παρεξηγήθηκε από την έγκυρη μαθηματική κοινότητα. Στο περιοδικό της Αγίας Πετρούπολης "Γιός της Πατρίδας" εμφανίστηκε ακόμη και ένα προσβλητικό σημείωμα: "Γιατί να γράφετε, ακόμη και να τυπώνετε, τέτοιες γελοίες φαντασιώσεις;" Και όλα αυτά γιατί στο άρθρο του, ο Λομπατσέφσκι αμφισβήτησε τη φαινομενικά προφανή δήλωση ότι μόνο μία ευθεία γραμμή μπορεί να τραβήξει ένα σημείο του επιπέδου που δεν τέμνει τη δεδομένη. Ο Νικολάι Ιβάνοβιτς στο μοντέλο του αντικατέστησε αυτή τη δήλωση με μια εντελώς αντίθετη: «Περισσότερες από μία ευθείες γραμμές μπορούν να συρθούν σε οποιοδήποτε σημείο,
Ακόμη και μετά από μια δεύτερη απόπειρα δημοσίευσης 10 χρόνια αργότερα, ο Λομπατσέφσκι λαμβάνει και πάλι μια αρνητική αξιολόγηση από τον Μιχαήλ Οστρογκράντσκι, μέλος της Ακαδημίας Επιστημών της Αγίας Πετρούπολης και αναγνωρισμένο ηγέτη των μαθηματικών στη Ρωσική Αυτοκρατορία εκείνη την εποχή. Τότε ο Λομπατσέφσκι αποφάσισε να παρουσιάσει τις ιδέες του σε ξένους επιστήμονες και αυτή η προσπάθεια ήταν αρκετά επιτυχημένη. Ο ίδιος ο «βασιλιάς των μαθηματικών» Καρλ Φρίντριχ Γκάους μίλησε καλά για τη νέα γεωμετρία, πάνω στην οποία δούλευε ο ίδιος τότε, αλλά και δεν τόλμησε να τη δημοσιεύσει λόγω του φόβου να καταδικάσει μια τόσο απίστευτη θεωρία. Αλλά δεν υπάρχει προφήτης στην Πατρίδα και η θέση του Λομπατσέφσκι δεν έχει βελτιωθεί. Στο τέλος της ζωής του, ο Νικολάι Ιβάνοβιτς χρεοκόπησε εντελώς, πούλησε το σπίτι του στο Καζάν και την περιουσία της συζύγου του. Και μόνο 10 χρόνια μετά το θάνατό του, οι καινοτόμες απόψεις του εκτιμήθηκαν από την παγκόσμια κοινότητα, και τα έργα του επιστήμονα μεταφράστηκαν σε όλες τις ευρωπαϊκές γλώσσες. Τι έχουμε τώρα; Η θεωρία της σχετικότητας δηλώνει ότι ακόμη και στον πραγματικό μας κόσμο, ο χώρος δεν είναι τόσο «λείος» όσο φαίνεται, ότι χρησιμοποιείται μια τροποποίηση του μοντέλου Lobachevsky για να τον περιγράψει. Το ίδιο μοντέλο, στο οποίο το άθροισμα των γωνιών ενός τριγώνου είναι μικρότερο από 180 μοίρες, στο οποίο το επίπεδο μπορεί να επιστρωθεί με κανονικά δεκάγωνα κ.λπ. Φαίνεται λοιπόν ότι η μαθηματική θεωρία, εντελώς αφύσικη και χωρισμένη από την πραγματικότητα, βρήκε τη θέση της! Αλλά στο άρθρο μου, θα μιλήσω για πιο συνηθισμένα πράγματα - για το πού μπορούμε να συναντήσουμε διαφορετικές μαθηματικές καμπύλες, πιθανότατα χωρίς καν να το γνωρίζουμε. ότι μια τροποποίηση του μοντέλου Lobachevsky χρησιμοποιείται για να το περιγράψει. Το ίδιο μοντέλο, στο οποίο το άθροισμα των γωνιών ενός τριγώνου είναι μικρότερο από 180 μοίρες, στο οποίο το επίπεδο μπορεί να επιστρωθεί με κανονικά δεκάγωνα κ.λπ. Φαίνεται λοιπόν ότι η μαθηματική θεωρία, εντελώς αφύσικη και χωρισμένη από την πραγματικότητα, βρήκε τη θέση της! Αλλά στο άρθρο μου, θα μιλήσω για πιο συνηθισμένα πράγματα - για το πού μπορούμε να συναντήσουμε διαφορετικές μαθηματικές καμπύλες, πιθανότατα χωρίς καν να το γνωρίζουμε. ότι μια τροποποίηση του μοντέλου Lobachevsky χρησιμοποιείται για να το περιγράψει. Το ίδιο μοντέλο, στο οποίο το άθροισμα των γωνιών ενός τριγώνου είναι μικρότερο από 180 μοίρες, στο οποίο το επίπεδο μπορεί να επιστρωθεί με κανονικά δεκάγωνα κ.λπ. Φαίνεται λοιπόν ότι η μαθηματική θεωρία, εντελώς αφύσικη και χωρισμένη από την πραγματικότητα, βρήκε τη θέση της! Αλλά στο άρθρο μου, θα μιλήσω για πιο συνηθισμένα πράγματα - για το πού μπορούμε να συναντήσουμε διαφορετικές μαθηματικές καμπύλες, πιθανότατα χωρίς καν να το γνωρίζουμε.
Καμπύλες ισχύος
Το απλούστερο παράδειγμα καμπύλης είναι, παραδόξως, μια ευθεία γραμμή. Τι είναι τελικά η ευθεία; Η ερώτηση δεν είναι τόσο απλή, γιατί αν προσπαθήσουμε να την απαντήσουμε, θα προκύψουν νέες έννοιες στην απάντησή μας, οι οποίες με τον ένα ή τον άλλο τρόπο θα χρησιμοποιήσουν τις ιδιότητες της ευθείας που είναι γνωστές σε εμάς. Αλλά στα μαθηματικά όλα είναι αυστηρά, και αποδεικνύεται ότι ο γεωμετρικός ορισμός της ευθείας γραμμής απλά δεν υπάρχει! Εισάγεται χωρίς ορισμό. Αλλά, νομίζω, κάθε αναγνώστης στο επίπεδο της διαίσθησης καταλαβαίνει τι είναι. Μια ευθεία γραμμή ονομάζεται καμπύλη πρώτης τάξης ή καμπύλη πρώτου βαθμού, δηλαδή δίνεται από μια εξίσωση πρώτου βαθμού σε καρτεσιανές συντεταγμένες, δηλαδή ax + κατά + c = 0.
Δεν θα σταθούμε όμως σε μια τόσο απλή περίπτωση. Μαζί με μια τέτοια «καμπύλη» όπως η «ευθεία γραμμή», οι αρχαίοι γεωμέτροι ξεχώρισαν έναν κύκλο ως «τέλεια καμπύλη». Ένας κύκλος είναι μια καμπύλη δεύτερης τάξης, που δίνεται από τη γνωστή εξίσωση: x 2 + y 2 = R 2. Ο ορισμός του μπορεί ήδη να δοθεί με πολλούς τρόπους, συγκεκριμένα, υπάρχει ένας γεωμετρικός ορισμός: "Ένας κύκλος είναι το σύνολο όλων των σημείων του επιπέδου που ισαπέχουν από ένα δεδομένο σημείο." Δεν χρειάζεται να μιλήσουμε για τη σημασία του κύκλου - τι αξίζει ο τροχός. Εδώ σχεδόν τελειώνουν οι μαθηματικές καμπύλες που μελετήθηκαν στο σχολείο, αν και υπάρχει ακόμα μία. Αυτή είναι η παραβολή που είναι γνωστή σε όλους στην άλγεβρα ως η γραφική παράσταση μιας τετραγωνικής συνάρτησης. Από αυτόν τον ορισμό, παρεμπιπτόντως, προκύπτει ότι μια παραβολή είναι επίσης μια καμπύλη δεύτερης τάξης, όπως ένας κύκλος. Στη συνέχεια, οι μαθητές συναντούν μια παραβολή στα μαθήματα φυσικής, εξετάζοντας ρίψεις σώματος υπό γωνία ως προς τον ορίζοντα, και στη συνέχεια ενώ μελετούν κοίλους και κυρτούς καθρέφτες και φακούς. Εκεί ήδη μιλάμε για κάποιες γεωμετρικές ιδιότητες της παραβολής. Αλλά πώς γενικά μπορεί κανείς να προσεγγίσει τη μελέτη της γεωμετρίας μιας παραβολής, αν όλα, αυτό που έχουμε είναι κάποιο είδος λειτουργίας εκεί; Πολλοί άνθρωποι γνωρίζουν ότι η παραβολή έχει επίσης έναν κλασικό γεωμετρικό ορισμό. Δηλαδή: "Μια παραβολή είναι ένα σύνολο όλων των σημείων ενός επιπέδου που ισαπέχουν από μια δεδομένη ευθεία και ένα δεδομένο σημείο." Αυτό το σημείο ονομάζεται εστία της παραβολής, και η ευθεία γραμμή ονομάζεται ευθεία της παραβολής.
Για παράδειγμα, αν πάρουμε τη γραφική παράσταση της συνάρτησης y \u003d x 2 , η εστίαση αυτής της παραβολής θα είναι το σημείο (0; 0,25) και ο προσανατολισμός θα είναι η ευθεία γραμμή y \u003d -0,25. Έτσι, μια παραβολή, όπως ένας κύκλος, μπορεί να εξεταστεί με ασφάλεια για γεωμετρικές ιδιότητες, οι οποίες, στην πραγματικότητα, είναι πολλές. Χωρίς να μπω σε λεπτομέρειες, θα πω ότι δεν είναι καθόλου προφανές ότι οι αλγεβρικοί και γεωμετρικοί ορισμοί δίνουν το ίδιο γεωμετρικό σχήμα. Η απόδειξη μπορεί να πραγματοποιηθεί χρησιμοποιώντας τη μέθοδο των συντεταγμένων.
Τώρα στο κύριο πράγμα - γιατί χρειαζόμαστε μια παραβολή; Ναι, ακόμα και για φακό! Και ακόμη περισσότερο, είναι απαραίτητο στην αστρονομία, στην οργάνωση των δορυφορικών επικοινωνιών, στη στρατιωτική και πολιτική βιομηχανία. Η πιο σημαντική ιδιότητα της παραβολής χρησιμοποιείται - η οπτική, όταν μια παράλληλη δέσμη φωτός, που αντανακλάται από την παραβολή, συλλέγεται ακριβώς στην εστία της και όλες οι ακτίνες φτάνουν στην εστία την ίδια στιγμή. Το αντίστροφο ισχύει επίσης: εάν τοποθετήσετε μια πηγή φωτός στο επίκεντρο της παραβολής, τότε, που αντανακλώνται από την παραβολή, οι ακτίνες θα είναι μια παράλληλη δέσμη φωτός. Είναι αυτή η πραγματικά φανταστική ιδιότητα που βασίζεται στη λειτουργία τηλεσκοπίων, δορυφορικών πιάτων και στρατιωτικών ραντάρ. Ας αποδείξουμε αυτή την ιδιότητα.
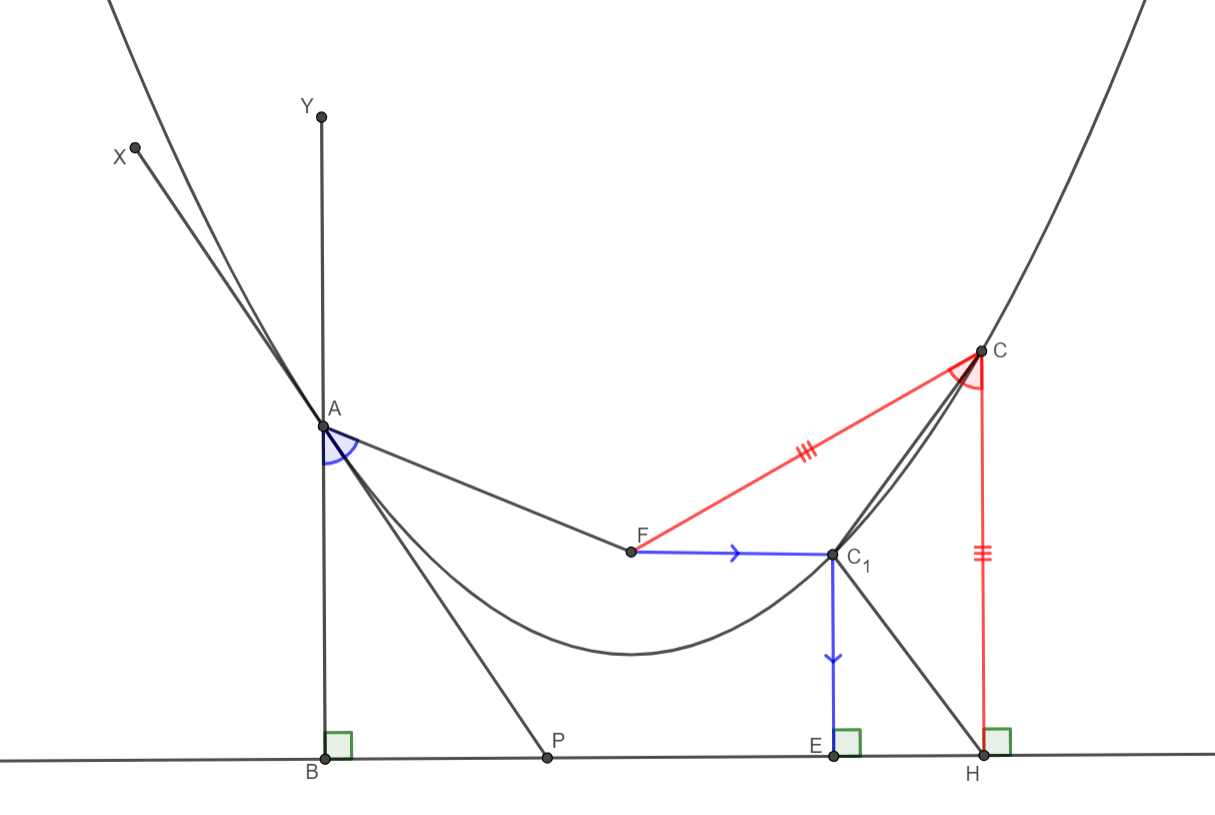
Η ανάκλαση του φωτός από την καμπύλη μπορεί να θεωρηθεί ως η ανάκλαση από την εφαπτομένη της καμπύλης σε αυτό το σημείο. Πάρτε κάποιο σημείο Α στην παραβολή και σχεδιάστε την εφαπτομένη XP μέσα από αυτήν. Είναι γνωστό από τη φυσική ότι η γωνία πρόσπτωσης είναι ίση με τη γωνία ανάκλασης, επομένως στόχος μας είναι να αποδείξουμε ότι η γωνία BAP (η οποία είναι ίση με τη γωνία XAY) είναι ίση με τη γωνία PAF, δηλαδή η εφαπτομένη στο Το σημείο Α είναι η διχοτόμος της γωνίας BAF. Ας υποθέσουμε ότι δεν είναι έτσι, τότε ας υπάρχει ένα σημείο C, και η διχοτόμος της γωνίας FCH τέμνει την παραβολή σε κάποιο σημείο C 1 . Τότε από τον ορισμό της παραβολής CF=CH, C 1 F=C 1 E. Αλλά ταυτόχρονα τα τρίγωνα FCC 1 HCC 1 είναι ίσα σε 2 πλευρές και γωνία, άρα FC 1 =HC 1 . Αποδείχθηκε ότι στο τρίγωνο EHC1 σκέλος ισούται με την υποτείνουσα, αλλά αυτό δεν συμβαίνει. Αυτό σημαίνει ότι η διχοτόμος της γωνίας FCH δεν τέμνει την παραβολή για δεύτερη φορά, δηλαδή την αγγίζει.
Ένα ενδιαφέρον γεγονός είναι ότι στα εγχειρίδια φυσικής, όταν αποδεικνύονται οι ιδιότητες των κοίλων και κυρτών κατόπτρων, παραμελούνται πολλές ασήμαντες αποκλίσεις, με αποτέλεσμα η υπό μελέτη επιφάνεια να έχει τόσο τις ιδιότητες μιας παραβολής όσο και τις ιδιότητες ενός κύκλου. Από αυτό μπορούμε να συμπεράνουμε ότι, αυστηρά μιλώντας, φακοί και καθρέφτες με όλες αυτές τις ιδιότητες απλά δεν υπάρχουν, δεν μπορούν να κατασκευαστούν. Ωστόσο, στην πράξη, αυτό το μειονέκτημα μερικές φορές μπορεί πραγματικά να παραμεληθεί.
Υπερβολή
Η επόμενη καμπύλη που θίγεται στο σχολείο είναι μια υπερβολή - η γραφική παράσταση της συνάρτησης y = k/x . Μια υπερβολή είναι επίσης μια καμπύλη δεύτερου βαθμού, αλλά πού είναι αυτή η δεύτερη μοίρα; Λαμβάνεται πολλαπλασιάζοντας και τις δύο πλευρές της εξίσωσης με x:
xy = k - ο συνολικός βαθμός των x και y είναι ίσος με δύο.
Η υπερβολή έχει τον δικό της γεωμετρικό ορισμό: «το σύνολο όλων των σημείων
του επιπέδου, το μέτρο της διαφοράς στις αποστάσεις από τις οποίες σε δύο δεδομένα σημεία, που
ονομάζονται εστίες, είναι σταθερό».
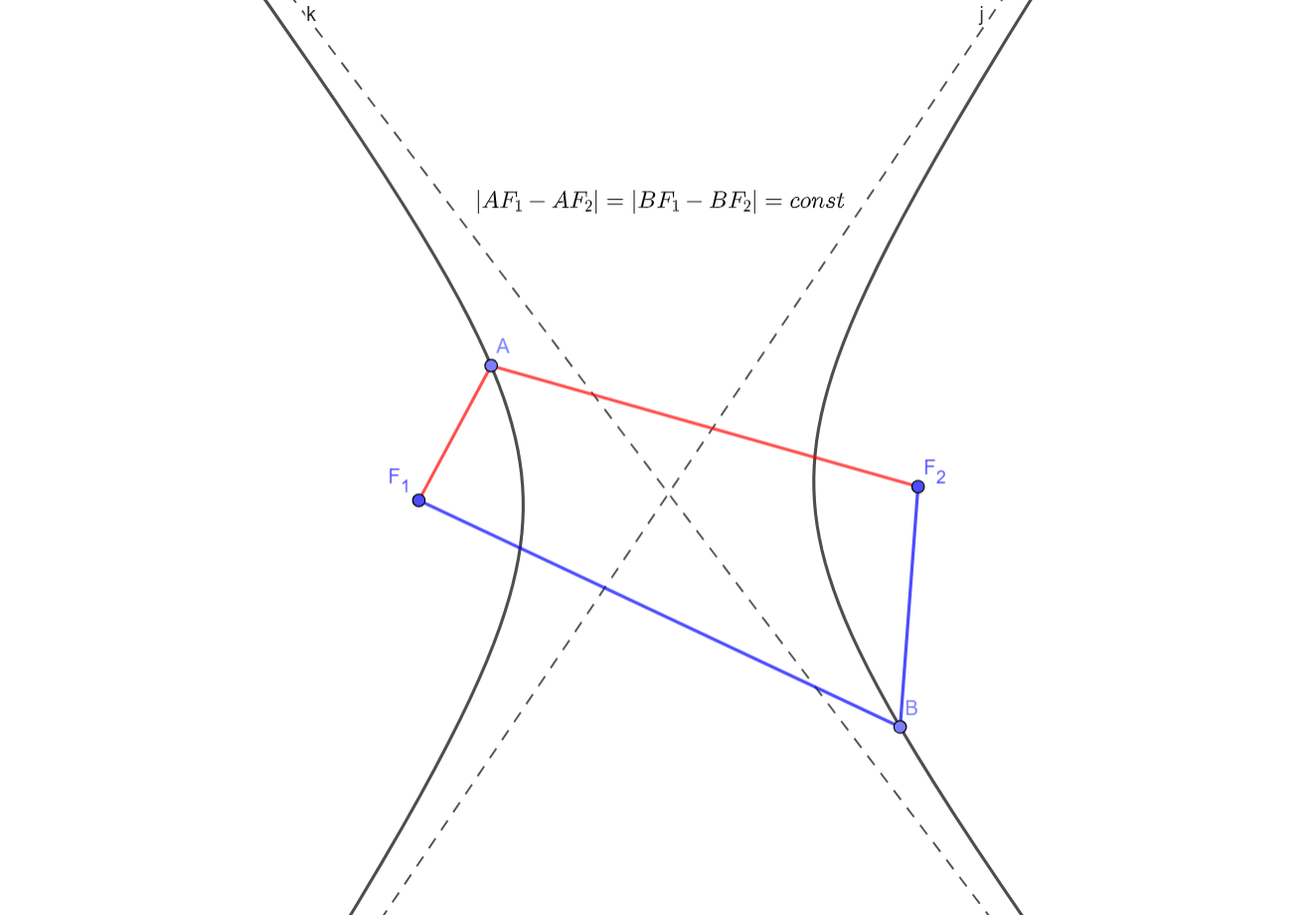
Ακούγεται τρομακτικό, αλλά η ουσία αυτού του ορισμού μπορεί να γίνει κατανοητή από την εικόνα. Οποιαδήποτε υπερβολή έχει 2 ασύμπτωτες - ευθείες γραμμές, στις οποίες η υπερβολή πλησιάζει, αλλά ποτέ δεν τις διασχίζει. Αν πάρουμε μια υπερβολή ως γραφική παράσταση της συνάρτησης y = k/x, τότε οι εστίες της θα είναι στα σημεία (√2; √2) και (-√2);- √2), και οι ασύμπτωτες θα είναι οι άξονες συντεταγμένων. Αλλά στη γενική περίπτωση, για μια υπερβολή, οι ασύμπτωτες μπορούν να σχηματίσουν οποιαδήποτε γωνία. Για παράδειγμα, η γραφική παράσταση της συνάρτησης y = x + 1/x είναι επίσης υπερβολή με ασύμπτωτες x = 0 και y = x, η γωνία μεταξύ των οποίων είναι 45⁰. Η υπερβολή έχει επίσης τη δική της οπτική ιδιότητα, την οποία θα αποδείξουμε λίγο αργότερα, γι' αυτό και χρησιμοποιείται σε ορισμένα τηλεσκόπια. Αλλά πιο συχνά, οι υπερβολές, όπως οι παραβολές, βρίσκονται στην αστρονομία, επειδή υπό την επίδραση των βαρυτικών δυνάμεων, σώματα με αρκετά υψηλή ταχύτητα πετούν κατά μήκος της υπερβολής. Π.χ,
Ελλειψη
Το τελευταίο παράδειγμα μιας καμπύλης δεύτερης τάξης είναι η έλλειψη, γνωστή ως η διαδρομή των πλανητών γύρω από τον ήλιο. Μπορεί να οριστεί με πολλούς τρόπους, ακόμη και ως «τεντωμένος κύκλος» κατά μία έννοια. Αλλά στη γεωμετρία, συνήθως χρησιμοποιείται ο ακόλουθος ορισμός: «Το σύνολο όλων των σημείων, το άθροισμα των αποστάσεων από τα οποία σε δύο δεδομένα σημεία, που ονομάζονται εστίες, είναι σταθερό». Πολύ παρόμοια με τον ορισμό της υπερβολής, μόνο η "διαφορά" αντικαθίσταται από το "άθροισμα", το οποίο φαίνεται πιο φυσικό, έτσι ώστε να μπορεί ακόμη και να σχεδιαστεί μια έλλειψη. Αρκεί να πάρετε 2 σκελίδες ή 2 βελόνες και να τις στερεώσετε στις εστίες της προβλεπόμενης έλλειψης, στη συνέχεια να τις βάλετε μια κλωστή, αλλά για να μην τεντωθεί, μετά πάρτε ένα μολύβι, τραβήξτε το νήμα με αυτό και, χωρίς να χαλαρώσετε την ένταση, τραβήξτε μια γραμμή. Τότε αυτή η γραμμή θα είναι έλλειψη.
Φυσικά, δεν μπορείτε να σχεδιάσετε μια έλλειψη σε ένα σημειωματάριο με αυτόν τον τρόπο, αλλά αυτό σας επιτρέπει να φανταστείτε και να νιώσετε την έλλειψη λίγο καλύτερα. Φυσικά, η έλλειψη έχει και τη δική της οπτική ιδιότητα. Εάν τοποθετήσετε μια πηγή φωτός στο επίκεντρο της έλλειψης, τότε μετά την ανάκλαση από τα τοιχώματα της έλλειψης, όλες οι ακτίνες θα συγκλίνουν σε άλλη εστία και ταυτόχρονα. Φυσικά, ο ρόλος του φωτός μπορεί να παίξει οποιαδήποτε κύματα, όπως ο ήχος. Ένα εντυπωσιακό παράδειγμα χρήσης αυτής της ιδιότητας είναι η μέθοδος της λιθοτριψίας στην ιατρική, κατά την οποία είναι δυνατή η αφαίρεση λίθων από τα νεφρά χωρίς χειρουργική επέμβαση. Ο ασθενής τοποθετείται σε ελλειπτικό λουτρό έτσι ώστε ο νεφρός με την πέτρα να βρίσκεται σε μία από τις εστίες του. Μια πηγή υπερήχων τοποθετείται σε άλλη εστία. Αντανακλώντας από τους τοίχους, ο υπέρηχος συλλέγεται σε ένα σημείο και καταστρέφει την πέτρα σε κατάσταση άμμου, η οποία μπορεί να φύγει από το σώμα φυσικά.
Αρχικά, χρειαζόμαστε ένα βοηθητικό πρόβλημα, γνωστό ως πρόβλημα Heron. Εάν υπάρχει μια ευθεία ΑΒ, καθώς και 2 σημεία P και Q στη μία πλευρά της, τότε πού στην ευθεία ΑΒ μπορεί κανείς να τοποθετήσει ένα σημείο Χ έτσι ώστε το άθροισμα PX + QX να είναι ελάχιστο; Ας αντικατοπτρίσουμε το σημείο Q σε σχέση με το AB, παίρνουμε το σημείο Q'. Τότε το επιθυμητό σημείο Χ βρίσκεται στην τομή του τμήματος PQ και της ευθείας ΑΒ. Πράγματι, πάρτε οποιοδήποτε άλλο σημείο Y στο ΑΒ, τότε από την ανισότητα του τριγώνου PY + Q'Y > PQ' = PX + XQ, δηλαδή, για οποιοδήποτε άλλο σημείο το απαιτούμενο άθροισμα είναι μεγαλύτερο από το σημείο X. Μπορεί να φανεί από την κατασκευή ότι οι γωνίες PXA είναι ίσες και QXB. Αυτό σημαίνει ότι το σημείο X είναι τέτοιο ώστε το φως που προέρχεται από το σημείο P, αφού ανακλαστεί από το AB στο σημείο X, χτυπά το σημείο Q.
Ας επιστρέψουμε στην έλλειψη. Πάρτε κάποιο σημείο A πάνω του και σχεδιάστε μια εφαπτομένη XY μέσα από αυτό. Θέλουμε να αποδείξουμε ότι οι γωνίες XAF 1 και YAF 2 είναι ίσες , δηλαδή ότι το σημείο Α στην ευθεία XY είναι το ίδιο σημείο από το πρόβλημα του Heron. Σημειώστε ένα άλλο σημείο στην εφαπτομένη της έλλειψης και συμβολίστε το ως Β. Εφόσον αυτό το σημείο βρίσκεται εκτός της έλλειψης, το άθροισμα των BF 1 και BF 2 είναι μεγαλύτερο από το άθροισμα των AF 1 και AF 2 (αυτό προκύπτει από τον ορισμό του έλλειψη). Επομένως, το σημείο A στην ευθεία XY είναι τέτοιο ώστε το άθροισμα των AF 1 και AF 2 είναι ελάχιστο, δηλαδή είναι ακριβώς το σημείο από το πρόβλημα του Heron. Και από αυτό το πρόβλημα γνωρίζουμε την απαιτούμενη ισότητα γωνιών.
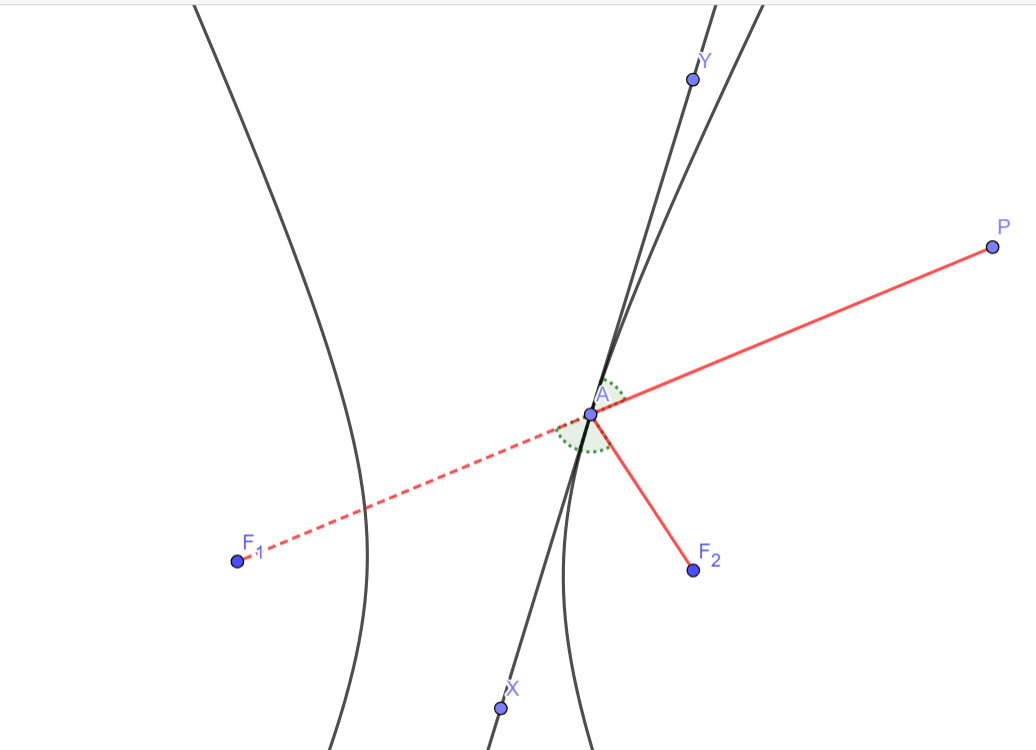
Η οπτική ιδιότητα μιας υπερβολής είναι παρόμοια με την ιδιότητα μιας έλλειψης και ακούγεται ως εξής: "Αν τοποθετήσετε μια σημειακή πηγή φωτός σε μια από τις εστίες της υπερβολής, τότε μετά από ανάκλαση από τον κλάδο της υπερβολής, οι ακτίνες θα πάνε σε τέτοια κατεύθυνση που οι συνέχειές τους θα διασταυρωθούν σε άλλη εστία». Όσον αφορά τη δεδομένη εικόνα, είναι απαραίτητο να αποδειχθεί η ισότητα των γωνιών XAF 1 και XAF 2 . Η απόδειξη αυτής της ιδιότητας είναι παρόμοια με την περίπτωση της έλλειψης, μόνο που το πρόβλημα του Heron θα πρέπει να τροποποιηθεί ελαφρώς. Εάν ενδιαφέρεστε, μπορείτε να προσπαθήσετε να κάνετε μόνοι σας το σκεπτικό.
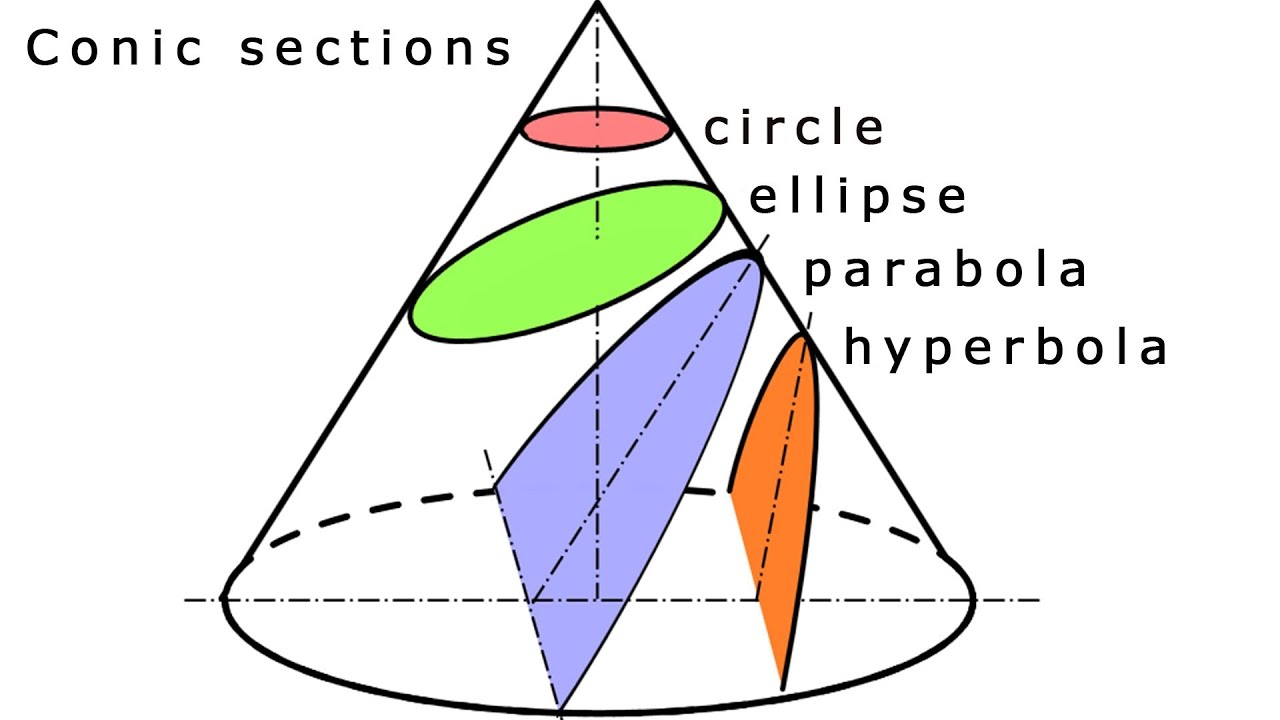
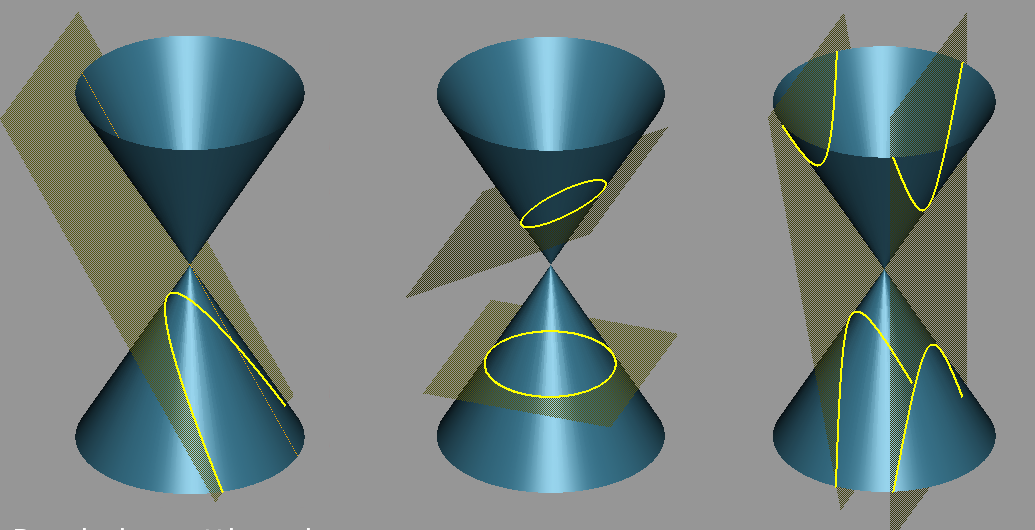
Γνωριστήκαμε λοιπόν με κάθε καμπύλη δεύτερης τάξης, αλλά έχουν κάτι άλλο κοινό; Αποδεικνύεται ότι υπάρχει. Εκτός από έναν μεγάλο αριθμό κοινών γεωμετρικών ιδιοτήτων, οποιαδήποτε από αυτές τις καμπύλες μπορεί να ληφθεί στην τομή ενός κώνου (ακριβέστερα, μια κωνική επιφάνεια) από ένα επίπεδο, γι' αυτό και ονομάζονται συχνά κωνικές .
Εάν το επίπεδο κοπής είναι παράλληλο με μία από τις γεννήτριες του κώνου, τότε λαμβάνεται μια παραβολή στην τομή (1η εικόνα). Εάν το επίπεδο τέμνει όλες τις γεννήτριες μόνο στο ένα "μισό", τότε προκύπτει έλλειψη (εικόνα 2). Και, τέλος, αν το επίπεδο τέμνει και τα δύο «μισά» του κώνου, τότε η τομή είναι υπερβολή, όπως στην 3η εικόνα. Ένας κύκλος θεωρείται έλλειψη με τις ίδιες εστίες. Φυσικά, τα κωνικά βρίσκονται τόσο στη γεωμετρία όσο και στη ζωή μας. Για παράδειγμα, η άκρη του ηλιακού ρολογιού κατά τη διάρκεια της ημέρας περιγράφει μια υπερβολή, οι κινήσεις των κοσμικών σωμάτων συχνά συμβαίνουν κατά μήκος ορισμένων κωνικών.
Άλλες καμπύλες ισχύος
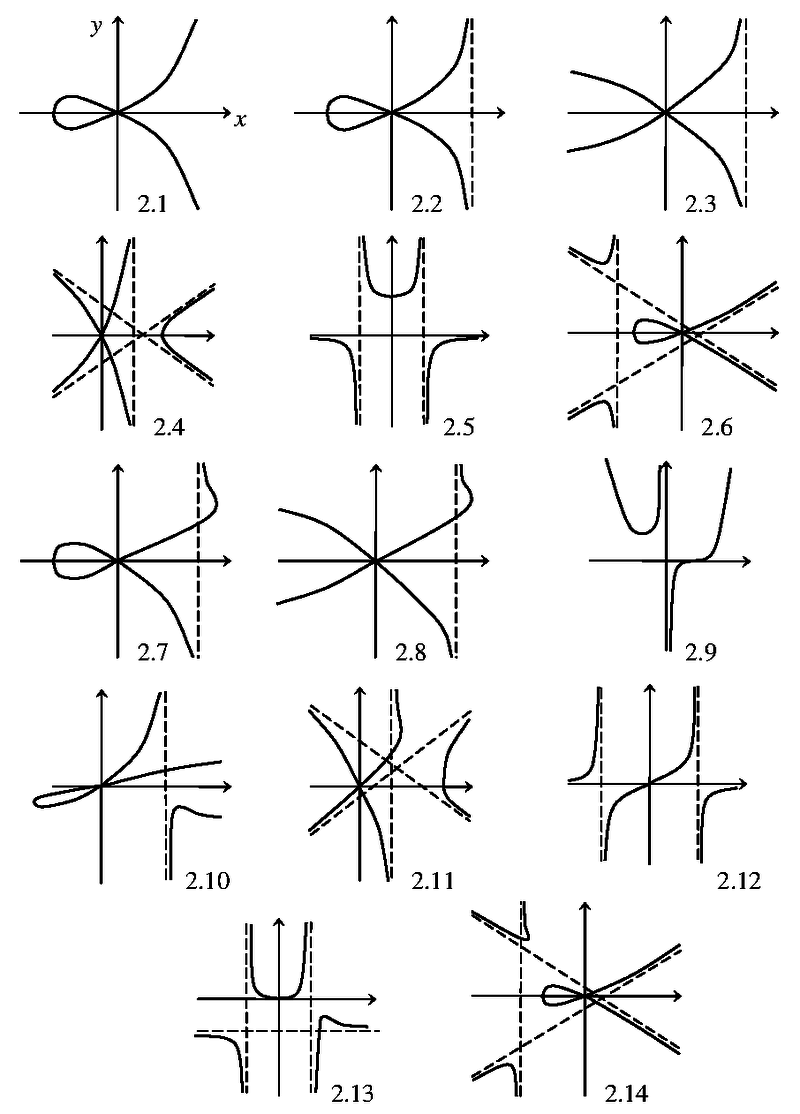
Όσο για τα άλογα, μπορούμε να σταματήσουμε εκεί. Ίσως, ενώ διάβαζε το άρθρο, ο αναγνώστης είχε μια ερώτηση: "Αφού υπάρχουν καμπύλες δεύτερου βαθμού, τότε πιθανώς και υψηλότεροι βαθμοί;" Ναι, οι καμπύλες μπορούν να έχουν οποιοδήποτε βαθμό, αλλά όσο υψηλότερος είναι ο βαθμός, τόσο περισσότεροι τύποι καμπυλών εμφανίζονται και τόσο λιγότερο βολικές είναι για μελέτη, επομένως δεν έχει νόημα να μιλάμε για καμπύλες βαθμού υψηλότερου από τον τέταρτο. Μετά τα κωνικά έρχονται καμπύλες τρίτου βαθμού ή κύβοι . Ένα απλό παράδειγμα κύβου είναι μια καμπύλη που είναι μια γραφική παράσταση της εξίσωσης y 2 + y - 2xy 2 = x 3 - x 2 . Όπως μπορείτε να δείτε, ο βαθμός κάθε όρου δεν ξεπερνά το 3.
Εάν υπάρχουν μόνο 3 τύποι κωνικών: έλλειψη, παραβολή, υπερβολή, τότε, έχοντας ανέβει μόνο ένα βαθμό προς τα πάνω, θα έχουμε περισσότερους από 50 διαφορετικούς τύπους κυβικών καμπυλών! Οι κυβικές καμπύλες, όπως και οι κωνικές, εμφανίζονται συχνά φυσικά στη γεωμετρία. Ανάμεσά τους, όμως, είναι λίγα τα ιδιαίτερα χρήσιμα. Ένα ειδικό είδος κυβικών καμπυλών, που ονομάζονται ελλειπτικές καμπύλες , έχει μεγάλη σημασία στην κρυπτογραφία και την κρυπτογράφηση δεδομένων, αλλά όλες οι ιδιότητές τους είναι πολύ περίπλοκες, επομένως δεν θα σταθώ σε αυτές.
Ωστόσο, υπάρχει μια τέτοια καμπύλη, που ονομάζεται κυβική παραβολή - το γράφημα της εξίσωσης y \u003d x 3 . Αυτή η καμπύλη μπορεί να βρεθεί σε οποιονδήποτε δρόμο, επειδή συχνά γίνονται στροφές σε μια κυβική παραβολή. Γιατί; Για να απαντήσετε σε αυτή την ερώτηση, πρέπει να πάτε λίγο βαθύτερα στην έννοια της καμπυλότητας μιας καμπύλης. Όσο μεγαλύτερη είναι η καμπυλότητα, τόσο μεγαλύτερη είναι η υπερφόρτωση που παρουσιάζεται κατά τη στροφή. Και για μια κυβική παραβολή, η καμπυλότητα αλλάζει σταδιακά, η οποία, αν και δεν μειώνει την υπερφόρτωση, την κάνει ομαλή. Στην πραγματικότητα, η κυβική παραβολή δεν είναι μια τέλεια καμπύλη για να στρίψετε, απλώς μοιάζει με αυτήν την τέλεια καμπύλη, για την οποία θα μιλήσουμε λίγο αργότερα, αλλά χρησιμοποιείται επειδή όλοι οι υπολογισμοί που σχετίζονται με αυτήν είναι πολύ πιο απλοί.
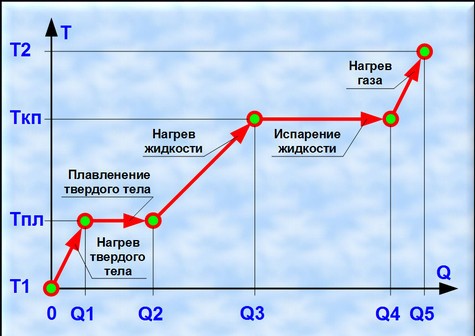
Τώρα θα μιλήσουμε για το πώς να χρησιμοποιήσουμε τις καμπύλες, για τις οποίες έχουμε ήδη μιλήσει. Υπάρχει κάτι σαν spline. Αν με απλό τρόπο, τότε πρόκειται για πολλές διαφορετικές καμπύλες που «ενώνονται» μεταξύ τους. Οι κυβικές καμπύλες χρησιμοποιούνται συχνά επειδή μπορούν να έρθουν σε όλα τα είδη των σχημάτων και βάζοντας μερικά κομμάτια μαζί μπορείτε να πάρετε σχεδόν τα πάντα. Αυτή η ιδιότητα των splines βρίσκει εφαρμογή στα γραφικά υπολογιστή. Οι σφήνες μερικές φορές περιγράφουν ορισμένες φυσικές διεργασίες. Για παράδειγμα, πώς θα ήταν ένα γράφημα της θερμοκρασίας του νερού σε σχέση με την εισροή θερμότητας; Πρώτον, το νερό θα θερμανθεί ανάλογα με την ποσότητα της θερμότητας, το γράφημα θα είναι μια κεκλιμένη ευθεία γραμμή, στη συνέχεια, όταν φτάσει τους 100 βαθμούς, η θερμοκρασία θα σταματήσει να αυξάνεται και όλη η θερμότητα θα πάει στον σχηματισμό ατμού, το γράφημα αυτής της διαδικασίας θα είναι ήδη μια οριζόντια ευθεία γραμμή. Και τέλος, όταν όλο το νερό εξατμιστεί, ο ατμός θα ζεσταθεί ξανά ανάλογα με την εφαρμοζόμενη θερμότητα. Το γράφημα αυτής της διαδικασίας είναι μια ευθεία γραμμή, αλλά έχει διαφορετική κλίση από το νερό. Έτσι, το γράφημα της όλης διαδικασίας είναι η απλούστερη spline, που αποτελείται από 3 ευθείες γραμμές. Εάν αρχικά δοθεί πάγος με αρνητική θερμοκρασία, τότε ο σφήνας θα αποτελείται ήδη από 5 μέρη.
Αυτό είναι το τέλος των καμπυλών ισχύος. Πριν μιλήσουμε για κάποιες άλλες καμπύλες, θα ήθελα να διευκρινίσω λίγο την έννοια της καμπυλότητας. Σε γενικές γραμμές, σχετίζεται στενά με την έννοια του παραγώγου, αλλά ας προσπαθήσουμε να το κάνουμε χωρίς αυτό, χρησιμοποιώντας μόνο τη διαίσθηση. Ας δούμε πρώτα ένα απλό παράδειγμα. Υπάρχει ένας κύκλος, είναι όλος συμμετρικός, όπως κι αν τον κοιτάξεις. Επομένως, η καμπυλότητα ενός κύκλου είναι ίδια σε όλα τα σημεία του. Εάν πάρετε μια υπερβολή, τότε πιο κοντά στο κέντρο θα είναι πιο «κυρτή» παρά σε κάποια απόσταση, όπου θα είναι σχεδόν δυσδιάκριτη από μια ευθεία γραμμή. Πώς όμως να μετρήσετε την καμπυλότητα μιας καμπύλης σε ένα αυθαίρετο σημείο; Αρκεί να προσεγγίσουμε αυτήν την καμπύλη με έναν συγκεκριμένο τρόπο κατά έναν κύκλο στο σημείο μας, τότε η καμπυλότητα της καμπύλης σε αυτό το σημείο θα είναι ίση με την καμπυλότητα ενός τέτοιου κύκλου. Αυτός ο κύκλος έχει καλή φυσική σημασία. Από το μάθημα της φυσικής είναι γνωστό2 ή R = v 2 / a. Έτσι, ο ίδιος ο κύκλος που προσεγγίζει καλύτερα την καμπύλη μπορεί να ληφθεί μετακινώντας το σώμα κατά μήκος της καμπύλης με σταθερή ταχύτητα και μετρώντας την επιτάχυνσή του στο επιθυμητό σημείο. Και, χρησιμοποιώντας την αναλογία για την κεντρομόλο επιτάχυνση, βρείτε την ακτίνα του κύκλου. Αυτή η ακτίνα ονομάζεται ακτίνα καμπυλότητας της καμπύλης στο δεδομένο σημείο. Όσο για την καμπυλότητα ενός κύκλου, αυτή είναι μια τιμή που είναι απλώς η αντίστροφη της ακτίνας του. Για παράδειγμα, ένας κύκλος με ακτίνα 2 cm θα έχει καμπυλότητα 1/2 = 0,5 cm -1 .
Έχουμε φτάσει κοντά στο να σκεφτούμε την ιδανική καμπύλη για στροφές στο δρόμο. Μια τέτοια καμπύλη ονομάζεται κλωθοειδής ή σπείρα Cornu . Είναι αξιοσημείωτο στο ότι η καμπυλότητά του αλλάζει ομοιόμορφα. Αυτό σημαίνει ότι εάν ο δρόμος είναι κατασκευασμένος με τη μορφή αυτής της σπείρας, τότε, ενώ οδηγεί κατά μήκος του, ο οδηγός θα στρίψει ομαλά το τιμόνι και αυτό θα επιτρέψει την είσοδο στη στροφή σχεδόν χωρίς να επιβραδύνει. Ωστόσο, ακόμη και από την εμφάνιση αυτής της καμπύλης, μπορεί κανείς να πει ότι δεν μπορεί να περιγραφεί με κάποια πρωτόγονη εξίσωση. Και επομένως, στην πράξη, συνήθως αντικαθίσταται από μια κυβική παραβολή.
Εξελίσσεται και εξελίσσεται
Σίγουρα έχετε αναρωτηθεί ποτέ τι μορφή έχει, για παράδειγμα, μια αλυσίδα που κρέμεται από δύο άκρες ή ένα σχοινί που κρέμεται ανάμεσα σε δύο στηρίγματα; Αυτή η καμπύλη ονομάζεται αλυσοειδές . Με την πρώτη ματιά, αυτή η καμπύλη μοιάζει με παραβολή, αλλά στην πραγματικότητα αυτή η καμπύλη δίνεται από μια εντελώς μη διαισθητική, αν και απλή, εξίσωση. Και συγκεκριμένα:
Το ch(x) είναι συνάρτηση του λεγόμενου υπερβολικού συνημιτόνου (μερικές φορές χρησιμοποιείται ο συμβολισμός cosh(x)), όπου e~2.72 είναι ο αριθμός Euler. Το τι σχέση έχει αυτή η συνάρτηση με την υπερβολή είναι ένα ξεχωριστό και πολύ ενδιαφέρον θέμα που σχετίζεται με τη γεωμετρία του Lobachevsky. Σε κάθε περίπτωση, δεν είναι καθόλου σαφές από πού προήλθε αυτή η φόρμουλα. Δυστυχώς, για να το αποδείξουμε, είναι απαραίτητο να λυθεί κάποια διαφορική εξίσωση, αν και όχι πολύ περίπλοκη, οπότε δεν θα δώσω την απόδειξη. Αλλά αυτή η καμπύλη μπορεί να χρησιμοποιηθεί και στην κατασκευή. Εάν αναποδογυριστεί, τότε η καμπύλη που λαμβάνεται με αυτόν τον τρόπο θα έχει ένα ιδανικό σχήμα για τη δομή της γέφυρας, δηλαδή εάν η γέφυρα έχει τέτοιο σχήμα, τότε το φορτίο στα στηρίγματα που τη στηρίζουν θα είναι ελάχιστο. Εάν το αλυσοειδές περιστρέφεται γύρω από τον άξονα συμμετρίας, τότε θα προκύψει μια επιφάνεια που είναι ιδανική για την κατασκευή θόλων.
Ωστόσο, το αλυσοειδές έχει λίγο περισσότερα κοινά με την παραβολή από την απλή εμφάνιση. Το αλυσοειδές μπορεί επίσης να ληφθεί ως η τροχιά της εστίας μιας παραβολής που κυλά σε ευθεία γραμμή χωρίς ολίσθηση. Ίσως κάποτε αναρωτήθηκε ο αναγνώστης: «Τι σχήμα πρέπει να έχει ο δρόμος για να μπορεί να κινείται σε τετράγωνους τροχούς χωρίς να κουνιέται;». Η απάντηση είναι ότι τα χτυπήματα στο δρόμο πρέπει να έχουν τη μορφή σωστά επιλεγμένων γραμμών αλυσοειδών.
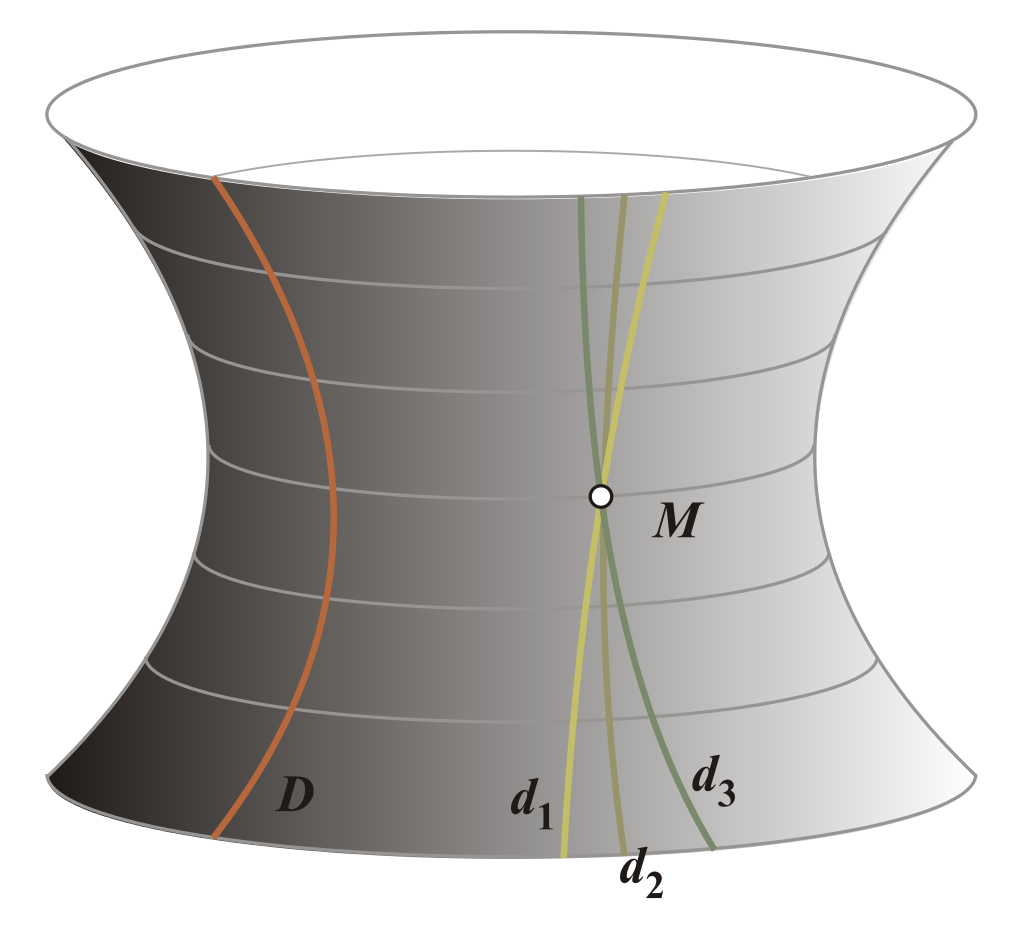
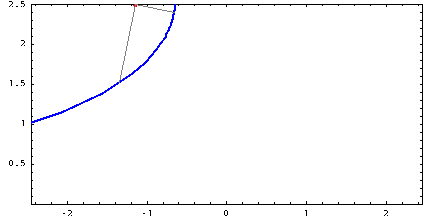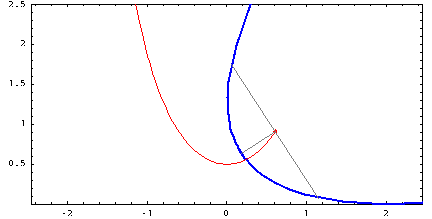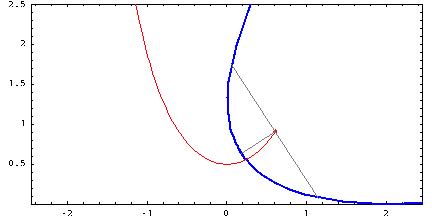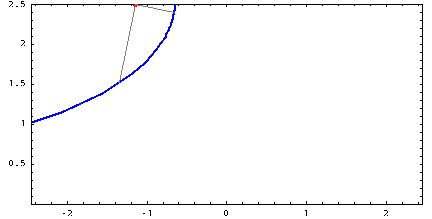
Στενά συνδεδεμένη με αυτή την αξιοσημείωτη καμπύλη είναι μια άλλη. Ας υπάρχει κάποια μη εκτάσιμη ράβδος που βρίσκεται στην επιφάνεια του τραπεζιού με αρκετά μεγάλη τριβή. Θα τραβήξουμε αργά τη μία άκρη της ράβδου κατά μήκος κάποιας ευθείας γραμμής όχι προς την κατεύθυνση της ράβδου. Τότε ποια τροχιά θα περιγράψει το άλλο άκρο; Μια τέτοια καμπύλη ονομάζεται tractrix . Αλλά έχει επίσης ένα άλλο, πολύ όμορφο όνομα - αλυσοειδές . Επίσης, αν περιστρέψουμε την τροχαλία γύρω από την ασύμπτωτη, θα έχουμε μια επιφάνεια που ονομάζεται ψευδόσφαιρα . Είναι αξιοσημείωτο στο ότι έχει μια σταθερή αρνητική καμπυλότητα, λόγω της οποίας είναι δυνατή η εφαρμογή της ήδη αναφερθείσας γεωμετρίας Lobachevsky σε αυτό.
Με την πρώτη ματιά, το tractrix δεν έχει καμία σχέση με τη γραμμή της αλυσίδας, επειδή η φυσική τους σημασία είναι εντελώς διαφορετική. Αλλά υπάρχει μια πολύ λεπτή και όμορφη μαθηματική σύνδεση μεταξύ αυτών των καμπυλών. Αν πάρουμε μια τροχιά, σημειώσουμε κάποιο σημείο πάνω της, σχεδιάζουμε μια εφαπτομένη της εφαπτομένης μέσω αυτής και στη συνέχεια σχεδιάζουμε μια κάθετη στην εφαπτομένη μέσω του ίδιου σημείου (αυτή η κάθετη ονομάζεται κανονική στην καμπύλη σε ένα δεδομένο σημείο), τότε θα αγγίξει κάποιο αλυσοειδές. Αυτή η σχέση μπορεί να απεικονιστεί με άλλο τρόπο: για κάθε σημείο του tractrix, σχεδιάζουμε έναν κύκλο καμπυλότητας (τον ίδιο κύκλο που προσεγγίζει καλύτερα την καμπύλη σε αυτό το σημείο) και μετά επισημαίνουμε τα κέντρα όλων αυτών των κύκλων. Όλα αυτά τα κέντρα σχηματίζουν ένα αλυσοειδές. Αν κάνουμε την ίδια πράξη, αλλά με αυθαίρετη καμπύλη, παίρνουμε μια άλλη καμπύλη, που ονομάζεται εξέλιξή της. Ετσι, το αλυσοειδές είναι η εξέλιξη του tractrix. Ένα βολβό είναι το ίδιο πράγμα, αλλά προς την άλλη κατεύθυνση. Δηλαδή, αν η καμπύλη Α είναι η συνέλιξη της καμπύλης Β, τότε η καμπύλη Β είναι η συνέλιξη της καμπύλης Α.
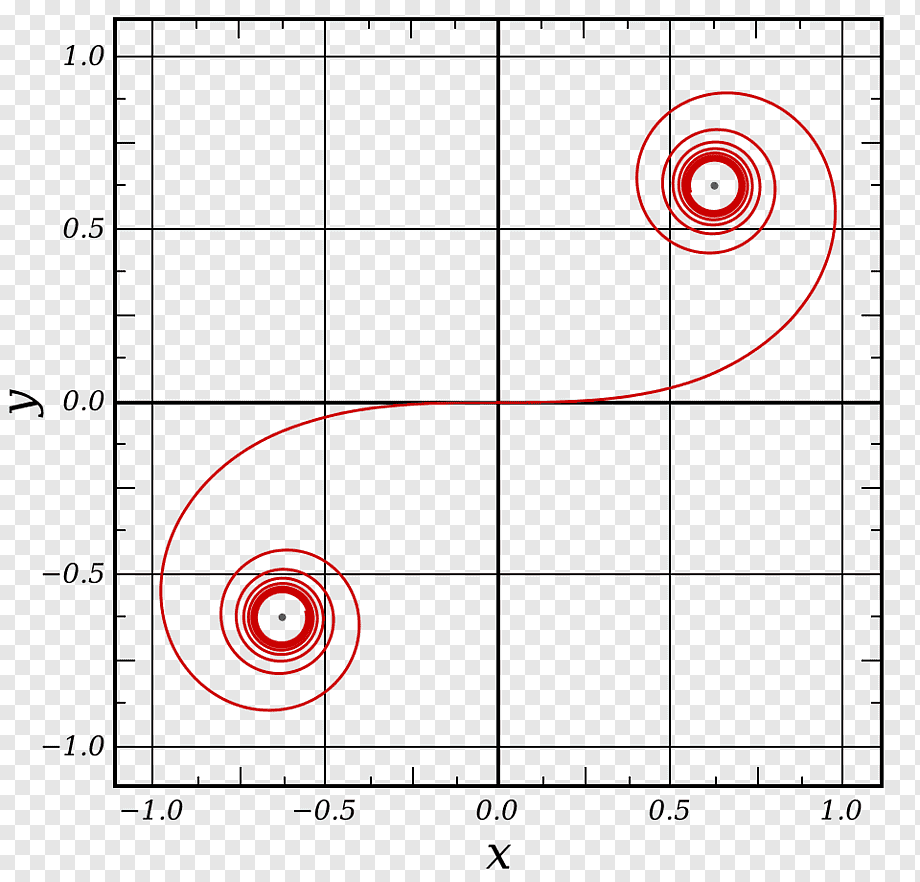
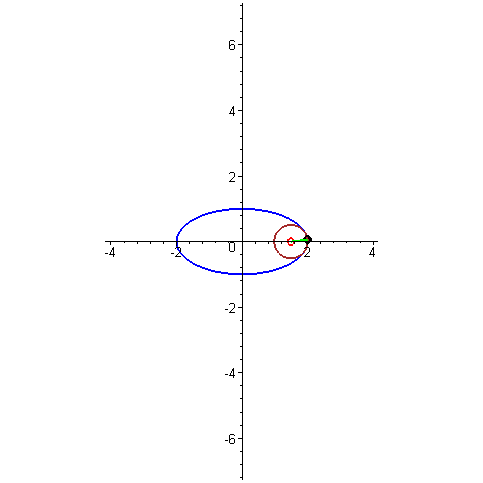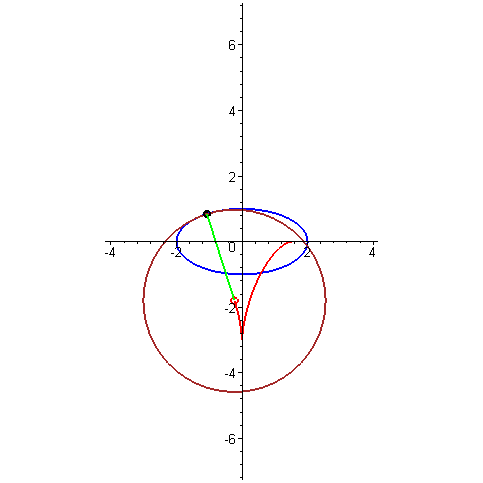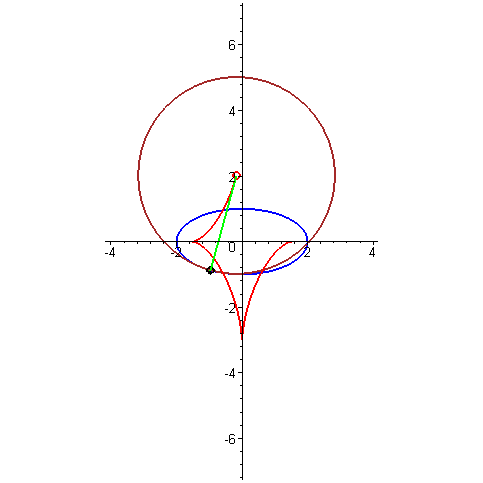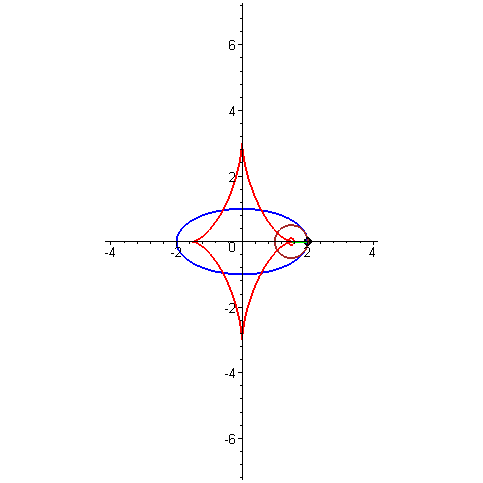
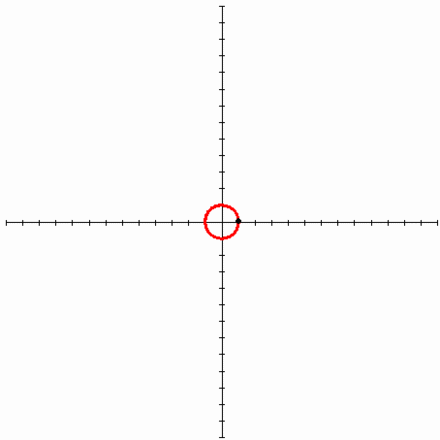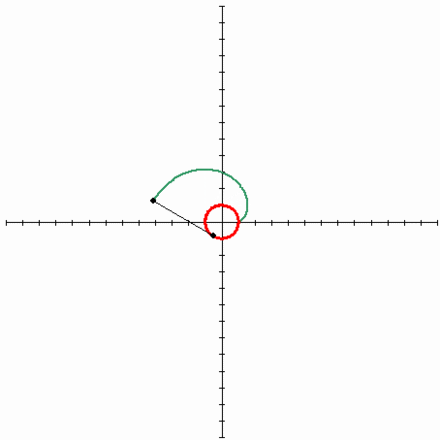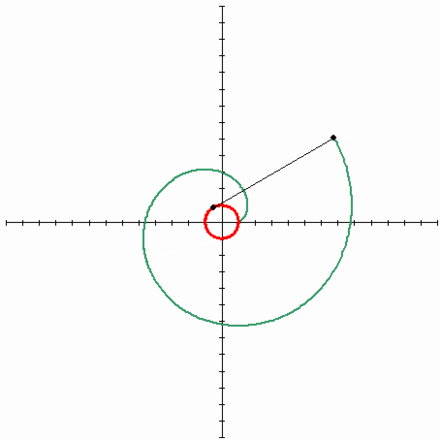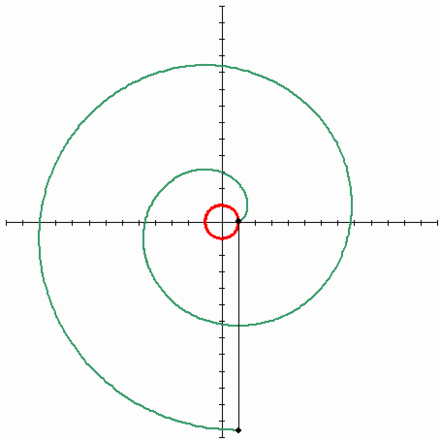
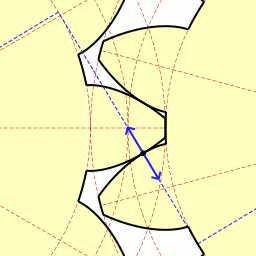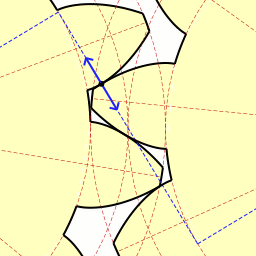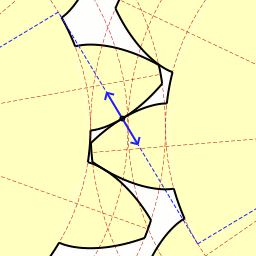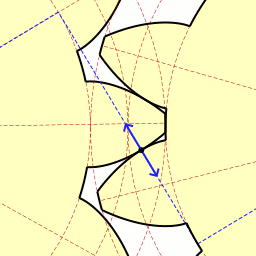
Τέλος, ήρθε η ώρα να μιλήσουμε για μια τόσο υπέροχη καμπύλη όπως η εξέλιξη ενός κύκλου . Μου αρέσει πολύ αυτή η καμπύλη, είναι κομψή και εύκολη στην κατασκευή. Αρκεί να στερεώσετε το καρούλι του νήματος σε κάθετη θέση και να αρχίσετε να ξετυλίγετε το νήμα, διατηρώντας το τεντωμένο. Στη συνέχεια, το άκρο του νήματος που βρίσκεται στο χέρι θα κινηθεί κατά μήκος της έλικας του κύκλου. Αυτή η καμπύλη έχει μεγάλη σημασία στο γρανάζια, γιατί αν τρίψετε τα δόντια στα γρανάζια κατά μήκος της περιέλιξης του κύκλου και παρατηρήσετε σωστά την απόσταση μεταξύ των γειτονικών δοντιών, θα έχετε ένα γρανάζι που λειτουργεί χωρίς να χτυπά. Αυτό σημαίνει ότι η επαφή μεταξύ των γραναζιών διατηρείται πάντα και επομένως και οι δύο ταχύτητες μπορούν να κινούνται ομοιόμορφα. Είναι αυτή η δέσμευση που είναι γνωστή ως involute.
συμπέρασμα
Φυσικά, υπάρχει ακόμα ένας τεράστιος αριθμός καμπυλών που εμφανίζονται με τον ένα ή τον άλλο τρόπο στη ζωή μας: μια λογαριθμική σπείρα, μια ημιτονοειδής, μια κυκλοειδής, μια λεμνική, μια βραχιστόχρονη κ.λπ. Αλλά θα τα πούμε κάποια άλλη στιγμή.
Πολλοί άνθρωποι δεν υποψιάζονται καν τι ένας καταπληκτικός κόσμος κρύβεται πίσω από μερικές φορές εγκόσμια πράγματα, και το όνομα αυτού του κόσμου είναι μαθηματικά. Στο άρθρο μου προσπάθησα να μυήσω τον αναγνώστη σε αυτό το παράλληλο σύμπαν, γεμάτο ομορφιά και αρμονία.
Ελπίζω να σας άρεσε το πρώτο μου άρθρο, θα χαρώ να κάνω εποικοδομητική κριτική)







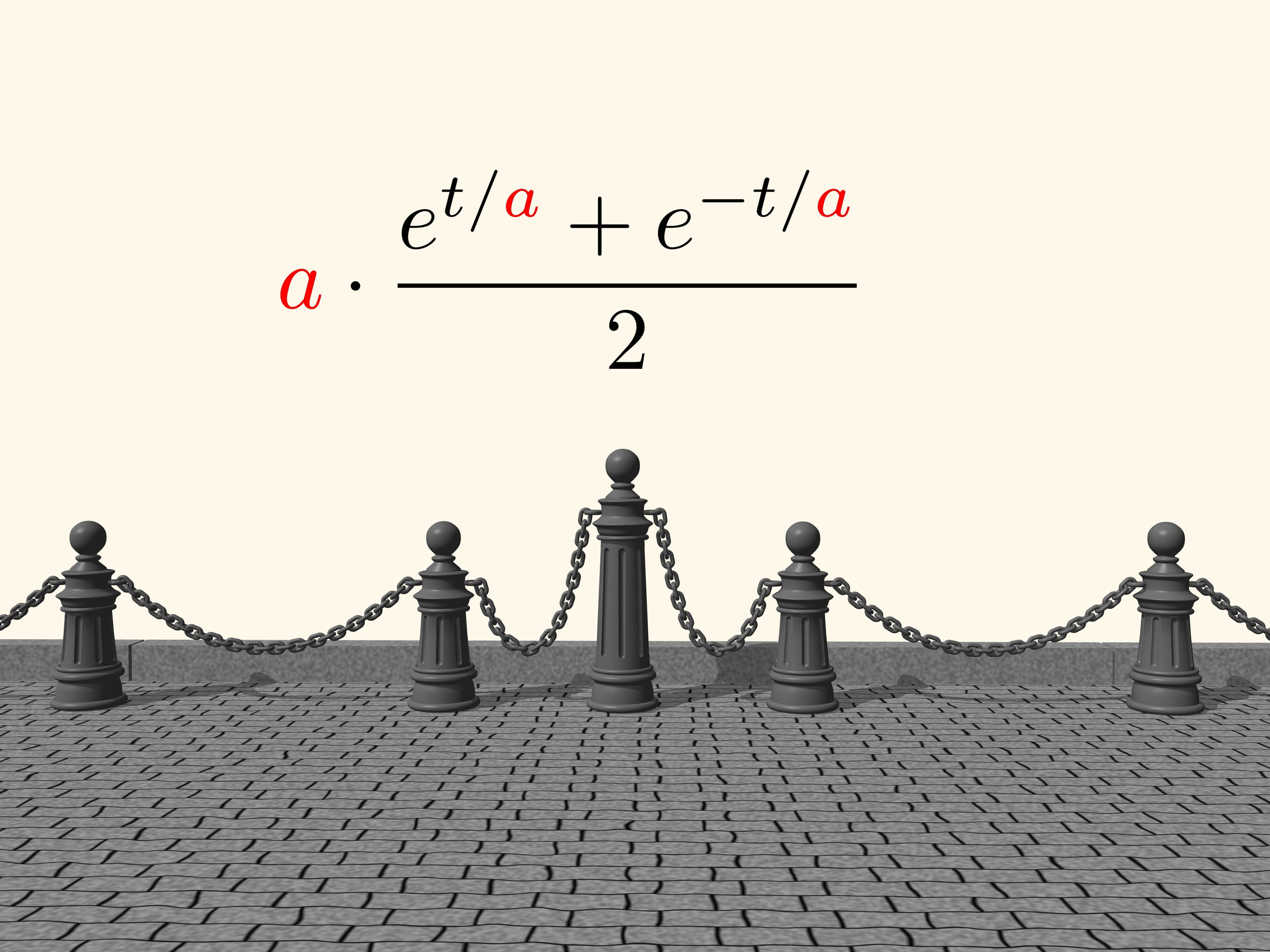


Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου