Μεθοδολογία στον Νόμος διατήρησης ενέργειας, με λυμένο παράδειγμα

Αλγόριθμος για την επίλυση προβλημάτων σχετικά με το νόμο της διατήρησης της ενέργειας:

1. Γράψτε μια σύντομη δήλωση του προβλήματος.
2. Μετατροπή μονάδων μέτρησης σε SI.
3. Επιλέξτε ένα σύστημα αναφοράς.
4. Προσδιορίστε τις αρχικές και τελικές θέσεις των σωμάτων, καθώς και, εάν χρειάζεται, τις ενδιάμεσες θέσεις που αναφέρονται στο πρόβλημα.
5. Επιλέξτε μηδενικό επίπεδο δυναμικής ενέργειας.
6. Εάν στα σώματα δρουν μόνο δυνητικές δυνάμεις, γράψτε τον νόμο διατήρησης της μηχανικής ενέργειας:     E ₁ \u003d E _2.  Εάν οι μη δυνητικές δυνάμεις δρουν επίσης στο σύστημα των σωμάτων, τότε γράψτε τον νόμο διατήρησης της ενέργειας με την ακόλουθη μορφή: Δ E \u003d E ₂ - E ₁ \u003d A,   όπου το A A είναι το έργο μη δυναμικών δυνάμεων.
7. Εκφράστε το άγνωστο.
8. Υπολογίστε την αριθμητική τιμή και τις μονάδες μέτρησης.
9. Αξιολογήστε το αποτέλεσμα.

 

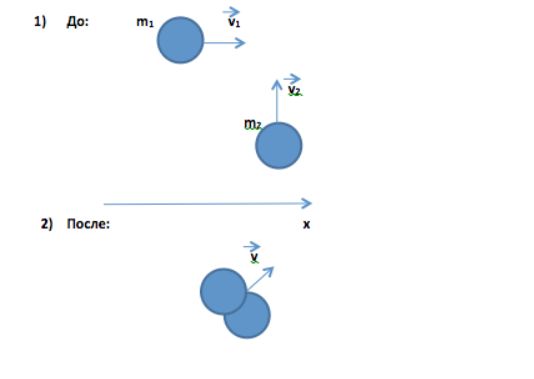
Γ2. Δύο μπάλες πλαστελίνης με μάζες 50 g η καθεμία κινούνται με τις ίδιες απόλυτες ταχύτητες 0,8 m/s, κατευθυνόμενες σε γωνία 90° μεταξύ τους. Ποιο μέρος της ενέργειας θα μετατραπεί σε θερμότητα σε μια τελείως ανελαστική σύγκρουση;

Λύση: 

Σε αδρανειακό πλαίσιο αναφοράς, υποθέτοντας το πλαίσιο                                                                                                                                                        

κλειστό. Νόμος διατήρησης της ορμής:

Ενέργεια του συστήματος πριν από την κρούση : E ₁ \u003d m ₁ v ₁ ² / 2 + m ₂ v ₂ ² / 2;  

 E ₁ \u003d 0,032 J

Η ενέργεια του συστήματος μετά την κρούση : E ₂ = ( m ₁ + m ₂ ) v ² /2;    E ₂ \u003d 0,016 J

Η ποσότητα θερμότητας που απελευθερώνεται κατά την κρούση:

Q \u003d E ₁ - E ₂    ;    Q = 0,016 J

Μέρος της ενέργειας που μετατρέπεται σε θερμότητα μετά την κρούση :  Q / E ₁ \u003d 0,5      

Απάντηση: 50%