Ένα ενδιαφέρον πρόβλημα για την περιοχή
Ο προγραμματιστής αποφάσισε να το κάνει όμορφο στο τετράγωνο οικόπεδό του: φτιάξε μια τετράγωνη αμμώδη περιοχή αναψυχής στο κέντρο, φτιάξε μια γωνιακή βεράντα κάτω αριστερά και πλακάκι μια στρογγυλή περιοχή κάτω από τη σχάρα μπάρμπεκιου στα δεξιά.Όταν πήγε για άμμο και πλακάκια, θυμήθηκε ήδη στο μαγαζί ότι είχε ξεχάσει να γράψει την περιοχή του κύκλου κάτω από το μπάρμπεκιου. Το μόνο που είχε ήταν ένα κομμάτι χαρτί με τέτοιο σχέδιο και η έκταση δύο άλλων οικοπέδων. Αλλά μετά από μερικά λεπτά, ο προγραμματιστής σχεδίασε ήδη τον απαιτούμενο αριθμό πλακιδίων. Πώς το έκανε;
===========================================================
Κατατακτήριες Αγγλικής
Προετοιμασία για τις Κατατακτήριες Εξετάσεις Αθήνας & Θεσ/νίκης με σταθερά εντυπωσιακά αποτελέσματα επί σειρά ετών!
Στήριξη των Πανεπιστημιακών Μαθημάτων για τους φοιτητές της Αγγλικής Φιλολογίας Αθήνας & Θεσ/νίκης!
Online Μαθήματα
Τα μαθήματα γίνονται on line με κέρδος χρόνου και άνεσης για τους υποψηφίους.
Η Προετοιμασία έχει πρακτικό χαρακτήρα, ΔΕΝ απαιτεί πολύωρη μελέτη, αναδιαρθρώνεται κάθε χρόνο και είναι προσανατολισμένη προς τις Εξετάσεις και όχι απλά στην κάλυψη της ύλης!100% Επιτυχία
Κάθε χρόνο τα ποσοστά επιτυχίας αγγίζουν το 100% των συμμετεχόντων μας αποδεδειγμένα με τα ΟΝΌΜΑΤΑ από το Πανεπιστήμιο και τις ΕΠΩΝΥΜΕΣ ΚΡΙΤΙΚΕΣ των επιτυχόντων μας και στις δύο πόλεις!
88 ΕΠΙΤΥΧΙΕΣ τα τελευταία 8 έτη
Για περισσότερες πληροφορίες πατήστε πάνω στην εικόνα
===========================================================
Το βασικό σημείο σε αυτό το πρόβλημα είναι ότι όλα τα γωνιακά τρίγωνα έχουν εμβαδόν 24. Αυτό συμβαίνει επειδή όλα αυτά τα τρίγωνα είναι ίδια. Ανεξάρτητα από το πώς περιστρέφουμε ένα τετράγωνο μέσα στο άλλο, όλα τα γωνιακά τρίγωνα θα παραμείνουν ίδια μεταξύ τους.
Εάν θέλετε να βεβαιωθείτε για αυτό με μεγαλύτερη ακρίβεια, μετρήστε τις απέναντι γωνίες σε τρίγωνα εάν η τιμή της αναπτυγμένης γωνίας είναι 180 °. Και αν τα τρίγωνα έχουν τις ίδιες γωνίες και τουλάχιστον μια πλευρά, αυτά είναι τα ίδια τρίγωνα.
Υπολογίζουμε επίσης αμέσως την υποτείνουσα του τριγώνου - είναι ίση με την πλευρά του κίτρινου τετραγώνου. Εφόσον το εμβαδόν ενός τετραγώνου είναι 100, τότε η πλευρά είναι √100 = 10.
==========================================================
Καλλιτεχνικό Βιβλιοχαρτοπωλείο - Δώρα - Διοργάνωση εκδηλώσεων - καλλιτεχνική δημιουργία -φωτοτυπίες
Για περισσότερα πατήστε πάνω στην εικόνα.
=====================================================
======
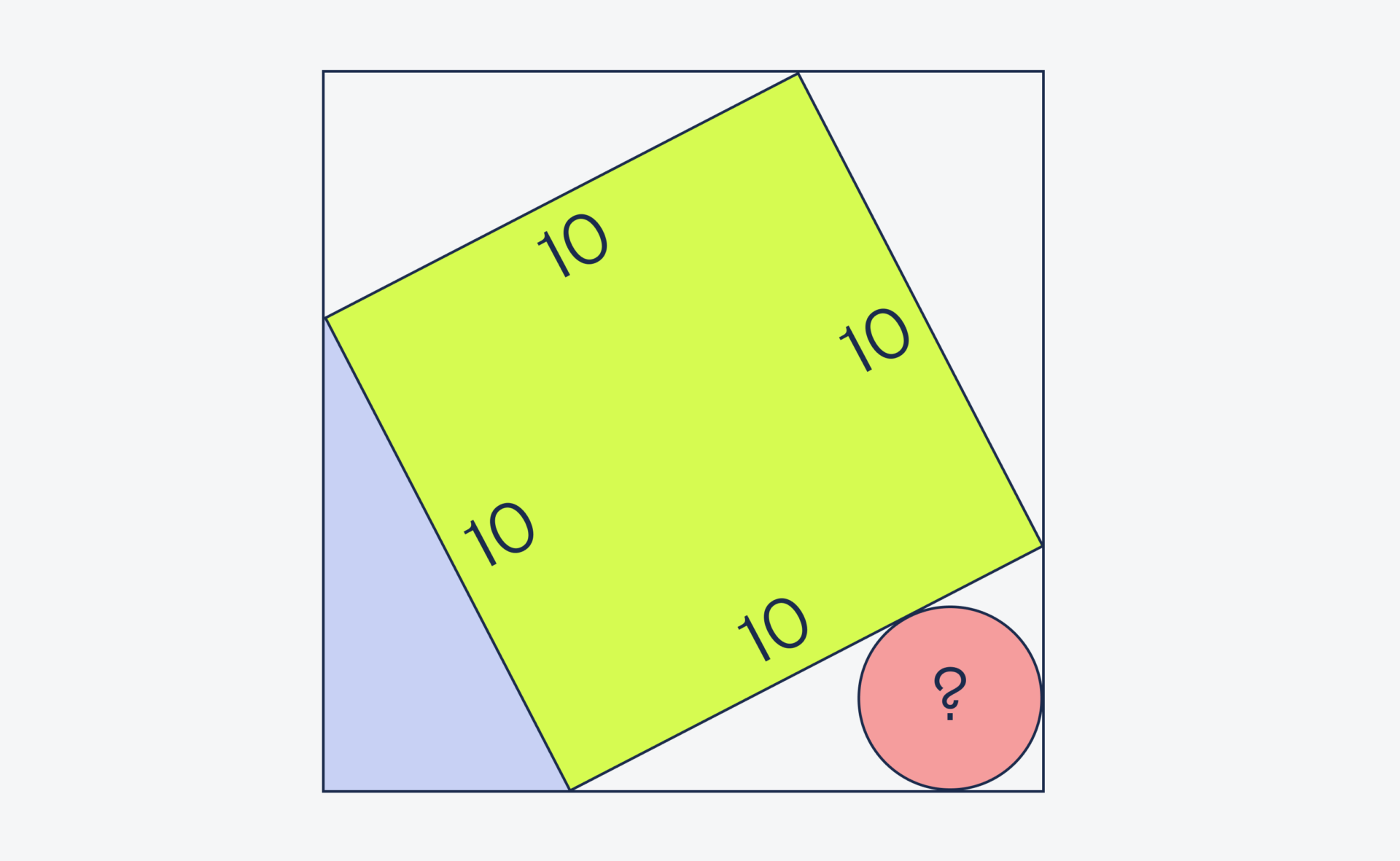
Τώρα ας ασχοληθούμε με τον κύκλο. Αποδεικνύεται ότι πρέπει να βρούμε το εμβαδόν ενός κύκλου εγγεγραμμένο σε ένα ορθογώνιο τρίγωνο του οποίου το εμβαδόν είναι 24 και η υποτείνουσα είναι 10.
Για το εμβαδόν ενός κύκλου, πρέπει να γνωρίζουμε την ακτίνα του. Καλούμε τον σχολικό τύπο για την ακτίνα ενός κύκλου εγγεγραμμένου σε ορθογώνιο τρίγωνο:
r = (a + b − c) / 2, όπου a και b είναι οι πλευρές του τριγώνου και c είναι η υποτείνουσα.
Γνωρίζουμε την τιμή της υποτείνουσας, βρίσκουμε το μήκος των δύο υπόλοιπων πλευρών. Το εμβαδόν ενός ορθογωνίου τριγώνου είναι (a × b) / 2, με αποτέλεσμα:
(a × b) / 2 = 24 → a × b = 48 → a = 48 / b
Τώρα ας εφαρμόσουμε τον τύπο από το Πυθαγόρειο θεώρημα, που λέει: a² + b² = c² και αντικαθιστούμε εκεί τις τιμές των a και c:
(48 / b)² + b² = 10²
2304 / b² + b² = 100
Εφόσον το εμβαδόν ενός τριγώνου είναι μη μηδενικό, αυτό σημαίνει ότι καμία πλευρά δεν είναι μηδέν, οπότε πολλαπλασιάζουμε και τις δύο πλευρές με b² για να απαλλαγούμε από τον παρονομαστή:
2304 + b4 = 100 × b² → b4 − 100 × b² + 2304 = 0
Συμβολίστε b² με x για να πάρετε τη συνηθισμένη τετραγωνική εξίσωση:
x² − 100 × x + 2304 = 0
===========================================================
Γαλλική Φιλολογία / Παν/ιακά Μαθήματα/Διπλωματικό Σώμα/ Κατατακτήριες-Α1-C2
+30 697 303 4528 Αποστολή μηνύματος st_kourneta@yahoo.gr
Το λύνουμε και παίρνουμε ότι x = 36 ή x = 64. Αυτό σημαίνει ότι:
b² = 36 → b = 6
b² = 64 → b = 8
Και αφού a × b = 48, αποδεικνύεται ότι:
a = 48 / 6 = 8
ή a = 48 / 8 = 6
Αυτό σημαίνει ότι οι πλευρές του τριγώνου έχουν διαστάσεις 6, 8 και 10. Αντικαταστήστε το στον τύπο για την εύρεση της ακτίνας:
r = (a + b − c) / 2 → r = (6 + 8 − 10) / 2 = 2
Τώρα εξετάζουμε το εμβαδόν του κύκλου - αυτός θα είναι ο αριθμός που χρειαζόμαστε:
S = π × r² → S = π × 4, που είναι περίπου ίσο με 12,56.
Αποδεικνύεται ότι ο προγραμματιστής πρέπει να πάρει 13 τετράγωνα του πλακιδίου.
Για περισσότερες πληροφορίες
Είμαστε πάντα κοντά στον μαθητή και στον φοιτητή.
Φροντιστηριακή Υποστήριξη με εξασφάλιση της επιτυχίας.
Πλήρης Φροντιστηριακή Υποστήριξη για μαθητές/.τριες και Φοιτητές /τριες
Ενημερωθείτε για τα οικονομικά πακέτα (μέχρι 30 ώρες τον μήνα ) σε ιδιαίτερα μαθήματα που οδηγούν με σιγουριά στην επιτυχία .
Αν χρειάζεσαι βοήθεια για την λύση των ασκήσεων ή έχεις οποιαδήποτε απορία πάτησε εδώ
Μην ξεχνάς ότι η μάθηση είναι θέμα κατανόησης και όχι παπαγαλίας !!!
Για περισσότερες πληροφορίες εδώ
Σου άρεσε? Μοιραστείτε το με τους φίλους σας!
Αν θέλεις να βλέπεις καθημερινά νέα άρθρα μπορείς να το κάνεις ακολουθώντας μας στο Facebook, ή επισκέψου την ομάδα υποστήριξης μαθημάτων στο Facebookκαι Instagram



Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου